Kompression im Allgemeinen

Sobald Daten übertragen/gespeichert werden (Speicherung ist nur eine Sonderform der Übertragung) wird Kompression zur Ressourcenausnutzung (Speicherplatz, Übertragungsdauer) unverzichtbar und ermöglicht bestimmte Anwendung überhaupt erst (bspw. digitales Video).

Die Idee zur Kompression ist älter als man denkt:

Im Mittelalter wurde in Klöstern, um die Schreibgeschwindigkeit zu erhöhen, häufig vorkommende Buchstabenkombinationen durch Einzelzeichen ersetzt. Erhalten haben sich unsere Umlaute.

Am Ende des 18. Jahrhunderts führte die britische Admiralität ein System zur Übermittlung von Befehlen an die Flotte ein - sechs Signalscheiben, die auf und zugeklappt werden konnten. Das ergibt 64 übermittelbare Kombinationen. Da für Buchstaben und Zahlen nur 36 notwendig sind, wurden die verbleibenden Kombinationen mit häufig vorkommenden Worten und Phrasen belegt.

1832: Samuel Morse stellte eine Statistik der Häufigkeit von Buchstaben in englischen Texten auf. Er ordnete dann den Buchstaben Kombinationen aus '.' und '-' zu, wobei die Übertragung von '-' dreimal solange dauerte wie die von '.'. Die häufigsten Buchstaben bekamen dann die kürzesten Kombinationen.

Ein bisschen Theorie und ein paar Begriffe

• Alphabet - eine Menge von Zeichen
• Wörter über einem Alphabet - Zeichenketten, bestehend aus Zeichen aus dem zugrundeliegenden Alphabet (die Menge der Wörter wird mit Σ^∗ bezeichnet)
• Quellen - Wortproduzenten (Sprecher, Sender, Datei, etc.)
• Quellen 0. Grades - gedächtnislose Quellen, Gesagtes (Gesendetes) beinflusst nicht das weiter Gesagte (Gesendete)
• Quellen n-ten Grades - Quellen mit Gedächtnis (Markov-Quellen)

Mit einem Quellalphabet Σ = {s₁,...,s_n}, n≥1, wobei jede Zeichen s_i die Häufigkeit p_i hat (p₁+...+p_n=1) spricht man von

• konstanter Quelle, wenn: es gibt ein Zeichen s_j∈Σ mit p_j=1 und für alle j≠i: p_j=0.
• zufälliger Quelle, wenn: für alle j=1,...,n: p_j=1/n, also ist jedes Zeichen gleich wahrscheinlich.
• geladener Quelle, wenn: ein "geladenes Zeichen" wird im Mittel jedes zweite Mal ausgewählt, alle anderen Zeichen sind gleich wahrscheinlich.

Entropie nach Shannon

Der Informationsgehalt eines Zeichens s aus einer Quelle mit dem zugrundeliegenden Alphabet aus n Zeichen ist definiert als I(s) = log_n(1/p(s)), im binären Fall (Alphabet {0,1}) ist das also:

I(s) = log₂(1/p(s)) = -log₂(p(s))

Je wahrscheinlicher (bzw. je häufiger) ein Zeichen vorkommt, desto weniger Informationsgehalt hat es also. Der Logarithmus überträgt dabei die Produkte von Wahrscheinlichkeiten (Zeichen s₁ UND s₂ treten auf) als additive Eigenschaft auf den Informationsgehalt (der wird übrigens dann in 1 sh (= 1 Shannon) gemessen).

Der durchschnittliche Informationsgehalt der Zeichen einer Quelle wird als Entropie bezeichnet (sie ist der Erwartungswert des Informationsgehalts der Zeichen):

H₁ = -∑_s∈Σ p(s) log₂(p(s)) für Quellen 0-ten Grades,

(weil es für Quellen höheren Grades umständlicher wird, verzichtet The Stophoto daher bei der prinzipiellen Betrachtung auf sie).

Für die obigen Quellen liefert das:

• zufällige Quelle: H₁ = log₂(n).
• konstante Quelle: H₁ = 0.
• geladenen Quelle: H₁ = 1 + (log₂(n-1))/2.

Für Wörter w der Länge n über dem Alphabet Σ definiert man analog: H_n= - Σ_w∈Σ^∗ p_w log(p_w), |w|=n. Die Quellenentropie ist dann definiert als lim_n→∞ H_n/n.

Fazit: ist eine Quelle gut vorhersagbar, wird die Entropie kleiner (bei der total vorhersagbaren konstanten Quelle ist sie 0), je mehr Zufall im Spiel ist, desto größer wird sie.

Was hat das mit Kompression zu tun? Ganz einfach:  verlustfreie Datenkompression versucht die Anzahl übertragener Zeichen (gemessen in Bits) zu verkleinern, bei gleichzeitiger Erhaltung der Information (gemessen in Shannons). Kompression war dann am wirksamsten, wenn sie jede Redundanz beseitigt hat und die durchschnittliche Bit-Anzahl der Entropie entspricht:  

Den Zusammenhang zwischen Entropie und durchschnittlich benötigter Bit-Anzahl zur exakten Übertragung von Zeichen eines Alphabets gibt das Source-Coding-Theorem von Shannon: bezeichnet b_s die Anzahl der Bits, die zum Kodieren von s benötigt wird, dann ist die durchschnittliche Anzahl, die zum Kodieren von Σ benötigt wird b = Σ_s∈Σ b_s p(s) und das Source-Coding-Theorem besagt dann, dass das optimale b (das kleinste, bei dem immer noch exakt, also verlustfrei übertragen werden kann) der Bedingung H₁ ≤ b ≤ H₁+1 gehorcht. Das Huffmann-Coding berechnet eine solche optimale Kodierung (Huffman 1954):

Statisches Huffman Coding

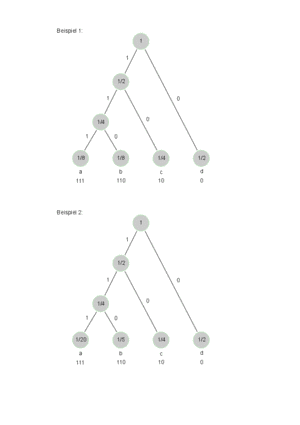
Dazu zwei Beispiele, in nebenstehender Skizze findet man die Huffman-Bäume dazu. Die Konstruktion der Bäume erfolgt so: für jedes Quellsymbol s erzeuge man einen Baum aus nur einem Blatt mit der Gewichtung p(s). Solange mehr als ein Baum vorhanden ist, wähle man die zwei Bäume mit kleinster Gewichtung, erzeuge eine Wurzel mit dem Gewicht als Summe der beiden Gewichte und hänge die beiden Bäume unter die neue Wurzel.

• 1. Beispiel: Σ = {a,b,c,d}; p(a)=0.5, p(b)=0.25, p(c)=0.125, p(d)=0.125: H₁=b=1.75
• 2. Beispiel: Σ = {a,b,c,d}; p(a)=0.5, p(b)=0.25, p(c)=2, p(d)=0.02, H₁=1.68, b=1.75

Beide Beispiele führen zur gleichen Kodierung, beim ersten wird sogar exakt die Entropieuntergrenze erreicht.

Neben dem statischen Huffman-Coding gibt es noch einige Erweiterungen, wie bspw. das adaptive Huffman-Coding. Huffmann Coding erreicht nicht immer das optimale Entropy Encoding (siehe die beiden Beispiele), dazu taugt das Arithmetic Coding oftmals besser, es soll aber hier nicht weiter erwähnt werden. Für Interessierte hat die Wikipedia einen Artikel parat.

Run-length Encoding

Dieses Verfahren ist gut geeignet für Bild-Kompression. Die Idee ist einfach: mehrfach vorkommende Zeichen werden durch ihre Anzahl ersetzt. Man kann das auch erweitern, indem man nach ganzen Mustern in der Quelle sucht und ihr Vorkommen zählt.

Weitere Kompressionsverfahren, wie z.B. Lempel-Ziv-Welsh (GIFs, Fax) und Lempel-Ziv-77 (gzip) bespricht The Stophoto nicht, weil sie für JPEGs nicht relevant sind.

Weiter zu JPEGs, DCT.