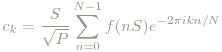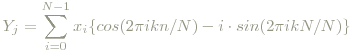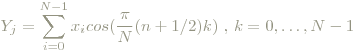Diskrete Cosinus-Transformation
Die diskrete Cosinus-Transformation (DCT) gehört zur Gruppe der Fourier- oder wenigstens "fourierartigen" Transformationen. Sie ist eng verwandt mit der diskreten Fourier-Transformation (DFT) und die wiederum ist, wie der Name schon andeutet, eine diskrete Ausgabe der ursprüngliche Fourier-Transformation.
Allen diesen Transformationen liegt die Idee zugrunde, eine Funktion oder ein Signal (also eine zeitlich Veränderliche Größe und damit auch nichts anderes als eine Funktion) in Komponenten zu zerlegen (um dann evt. darunter die Spreu vom Weizen zu trennen). Man denke an die Stereoeanlage, wo zuckende Balken die momentanen Frequenzanteile des Audiosignals anzeigen - da steckt eine solche Transformation dahinter.
Die Fourier-Reihe zerlegt periodische Funktionen mit endlicher Periode in eine Summe von Cosinus- und Sinus-Funktionen (auch Fourier-Komponenten genannt) unterschiedlicher Frequenz. Die Fourier-Transformation verallgemeinert das insoferne, als sie auch nicht-periodische Funktionen zerlegt, was als Übergang zu Funktionen mit unendlich langer Periode verstanden werden kann.
Die diskreten Varianten unterscheiden sich nun darin, dass das Signal (die Funktion), das (die) sie zerlegen wollen, nur in bestimmten (Zeit)Punkten gegeben ist (zeitdiskrete Fourier-Transformation) und die DFT kommt dabei sogar mit einer endlichen Liste von Werten aus. Die Zerlegeung eines solchen Signals, kann man natürlich auch mit der Fourier-Reihe/Fourier-Transformation tackeln. Dabei bekommt man allerdings Scheinkomponenten, also Frequenzanteile, die im Ausgangssignal nicht vertreten waren: ein Sinuston der von Ewigkeit zu Ewigkeit schwingt ist nun einmal mathematisch nicht das selbe wie ein Sinuston, der nur 10 Sekunden ertönt, und genau das führt dann zu Komponenten in der Zerlegung, die beim Anhören schlicht nicht da waren. Die "diskreten" Ansätzte dienen dazu, dieses Problem zu lösen. Im Folgenden noch eine Zusammenfassung für Eingeweihte.
Die Fourier-Reihe
Eine periodische Funktion f(x) mit der Periode P kann folgendermaßen zerlegt werden:
Die ck kodieren den Anteil der Frequenz k. The Stophoto erinnert außerdem an eikx = cos(kx) + i sin(kx).
Das Fourier-Integral
Verallgemeinert man auf nicht-periodischen Funktionen, bekommt man das durch die Fourier-Transformierte gegebene kontinuierliche Frequenzspektrum.
Die diskrete Fouriertransformation
Gegeben sei eine Folge (komplexer Zahlen) x0,...,xN-1, die DFT konvertiert sie gemäß
zu einer neuen Folge Yj. Man erkennt schon die Ähnlichkeit zu den Fourierkoeffizienten von vorher (Integral → endliche Summe). Diese Ähnlichkeit lässt sich begründen, denn man kann zeigen, dass die DFT-Koeffizienten eines endlichen diskreten Signals (xi)i=0,...,N-1 proportional zu den Koeffizienten der Fourierreihe des Signals (der Funktion) sind, das man erhält, wenn man die xi's interpoliert und das interpolierte Intervall periodisch fortsetzt. Im weiteren wird der Terminus Signal statt Funktion verwendet und für x die Zeit gedacht.
Um Aliasing (wenn ein kontinuierliches Signal zu grob abgetastet (gesampelt) wird, kann das bei Rekonstruktion des kontinuierlichen Signals aus dem Sample zu einem Signal mit niedriger Frequenz führen) zu vermeiden, muss dabei eine Voraussetzung erfüllt sein: das ursprüngliche Signal muss bandlimitiert sein (analytisch exakt: das Frequenzspektrum hat einen kompakten Träger), und zwar auf höchstens die Hälfte der Sampling-Rate des diskreten endlichen Signals (Nyquist–Shannon Sampling Theorem, siehe z.B. Sampling Theory, wer es genau wissen möchte).
Hat man also ein bandlimitiertes periodisches Signal f(x) mit ω⋅S ∈ (-π,+π) , wobei ω = 2π⋅f und S das Sampling-Intervall (der Abstand zweier Sample-Punkte) ist, kann man das Sampeln folgendermaßen formulieren: man multipliziere das Signal f(x) mit dem Filtersignal φ(x) = S⋅∑n=-∞..+∞δ(x-nS), wobei δ(x) die Diracsche Delta-Distribution ist. Das Sample-Signal ist dann fs(x)=f(x) φ(x).
Jetzt bestimmt man die "normalen" Fourierkoeffizienten dieses Signals mit der Formel für die kontinuierliche Fourier-Reihe und bekommt wegen der Eigenschaft der Delta-Distribution (The Stophoto erinnert: ∫a..bδ(x)f(x)=f(0), a≤0≤b) und Beschneidung der Sampledauer auf eine Periode P (n=0..[S/P]-1)
Wenn nun das Sampling-Intervall S ein Teiler der Periode P ist, also N=P/S ganzzahlig, wird das zu
und das entspricht bis auf den Vorfaktor der weiter oben definierten DFT.
Die diskrete Cosinus-Transformation (Typ II)
Mit der Eulerschen Formel kann man die DFT auch folgendermaßen schreiben:
Legt man eine symmetrische Fortsetzung des Signals außerhalb des gesampelten Bereichs zugrunde, fällt die asymmetrische Komponente in Form des Sinus-Anteils weg. Das ist die Grundlage der DCT (nebenbei: es gibt natürlich aus das quasi Gegenteil - die diskrete Sinus-Transformation). Je nachdem, wie man diese symmetrische Fortsetzung genau angibt, unterscheidet man 8 Typen der DCT. Die meistverwendete ist die vom Typ II:
Das entspricht exakt einer DFT folgender Signalfolge: y0,...,y4N, wobei y0=y2=...=y2N=0, y1=x0,...,y2N+1=xN und wegen der geraden Symmetrie y4N+n=yn, 0<n<2N. Das eingesetzt in die Formel für die DFT, ergibt die Formel für die DCT Typ II.



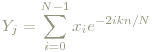
![c_k = \frac{1}{\sqrt{P}} \sum_{n=0}^{[S/P]-1} \int_0^P f(x)\delta(x-nS)e^{-2πikx/P}dx = \frac{S}{\sqrt{P}} \sum_{n=0}^{[S/P]-1} f(nS)e^{-2πiknS/P}](typo3temp/math/fb693f244f01646319b0c061e7489883.png)