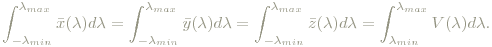Zu Farbsehen, Photometrie und Strahlung, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile
Das CIE-Normvalenzsystem von 1931
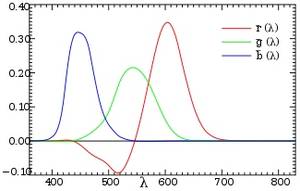
- Abb 1: Die rgb-Empfindlichkeitskurven des CIE 1931 Normalbeobachters (Quelle: Wikipedia)
Die Ergebnisse der folgenden vereinfachten Diskussion wurden 1931 von der Commission internationale de l'éclairage (CIE) zum Standard erklärt.
Dass die hier erfolgende willkürliche Festlegung dreier Grundfarben und die Ermittlung der zugehörigen Farbemfindlichkeitskurven und die sich daraus ableitende, auch mehr oder minder willkürliche Farbvalenz (mit den tatsächlichen physiologischen Erregungszuständen hat sie primär nichts zu tun) funktioniert, verdanken wir den Grassmanschen Gesetzen, siehe unter "Farbsehen". Und diese wiederum verdanken wir den physiologischen und psychologisch-neurologischen Mechanismen des Farbsehens, also sekundär doch auch u.a. den "echten" Erregungszuständen der Zapfen. Naja - kurz: unser Farbsehen ist eben derart gebaut, dass wir so vorgehen können, wie wir es hier tun werden.
Statt also die physiologischen Empfindlickkeitskurven der Zapfen (s. "Farbsehen, Abb. 1") zur Festsetzung der Tristumulus-Werte und damit als Farbäquivalent zu verwenden, werden drei mehr oder weniger beliebige Primärfarben herangezogen (3 Grundfarben genügen - erstes Grassmansches Gesetz, siehe unter "Farbsehen").
Die Bestimmung der Empfindlichkeitskurven aus Abb. 1 für die drei gewählten Grundfarben der Wellenlängen 700 nm (rot), 546.1 nm (grün) und 435.8 nm (blau) - die Auswahl der drei Wellenlängen geschah damals aus Günden der Praktikabilität bei der Herstellung von Lichtern dieser Frequenzen - geschieht dabei folgendermaßen (siehe Referenzen, The Stophoto vereinfacht ein wenig): der Normalbeobachter unternimmt ein Vergleichsexperiment - auf einen in 2 Hälften unterteilten kreisförmigen Schirm (mit Blickwinkel 2°) wird auf eine Hälfte monochromatisches Licht mit der Wellenlänge λ projiziert, auf die andere eine Mischung aus den drei gewählten Primärfarben. Der Beobachter passt nun die Helligkeit der Primärfarben durch Drehen von Reglern solange an, bis er Übereinstimmung mit der Spektralfarbe erreicht und notiert die notwendigen Helligkeitsanteile. In Fällen, wo er keine Gleichheit mit der Testfarbe erreichen kann, projiziert er eine der Primärfarben anstatt in den Mischbereich über die Testfarbe und variiert die Helligkeiten wieder, bis er so Übereinstimmung erzielt. In diesem Falle zählt er den Anteil der über die Testfarbe gemischten Primärfarbe als negativ. Variiert der Beobachter schließlich die Wellenlänge der Testfarbe über den sichtbaren Bereich des Spektrums, erhält er die Empfindlichkeitskurven aus Abb. 2. Dass es dabei genügt, nur die Spektralfarben heranzuziehen, liegt wieder an den Grassmannschen Gesetzen: jede Spektralverteilung (also beliebige Farbe) ist die additive Mischung seiner monochromatischen Anteile, die wiederum die Mischung der drei Primärfarben sind - Additivität wo man hinsieht, im wahrsten Sinne des Wortes.
Das ganze nun ein wenig technischer, aber genauer: was der Normalbeobachter für jede Wellenlänge notiert hat, ist idealerweise der RGB-Anteil einer "monochromatischen Verteilung" (Strahlungsleistung pro Meter (Wellenlänge), siehe "Photometrische Größen") der Form
Das entspricht einer spektralen Verteilung der Strahlungsleistung Φ0 mit einem singulären Peak bei λ0, angegeben in Watt/Meter. δ(x) ist dabei die Diracsche Delta-Distribution. Man möge sich an ihrere Stelle eine hinreichend schmale (bspw. 1nm beite) hohe einsame Zacke mit der darunterliegenden Fläche Φ0 vorstellen, was der Realität nahekommt.
Dem durch diese Verteilung verursachten Farbeindruck wird das RGB-Tripel (seine Werte gemessen in Watt) zugeordnet:
Um nicht die an sich beliebig wählbare Leistung Φ0 der monochromatischen Verteilungen mitzuschleppen, normiert man:
Durch die Normierung sind die Werte dimensionslos geworden, insbesonders ist bspw. ρ(λ700nm) =ϒ(λ546.1nm) =β(λ435.8nm)=1.
Schreibt man nun eine beliebige Spektralverteilung als
also als "kontinuierliche Summe" (die Integration über negative Wellenlängen ist kein Problem, da die Verteilungen dort verschwinden) von gewichteten monochromatischen Verteilungen, sieht man nun, dass jeder beliebigen Verteilung wegen der Grassmanschen Gesetze R-, G- und B-Werte zuordenbar sind, die dann selbst wieder additiv sind:
Es ist nämlich
Dabei steht das Symbol "⊕" links für die additive Mischung der Verteilungen, die sich durch unsere, die Grassmanschen Gesetze kodierenden Festlegungen auf eine arithmetische Addition im Raum der RGB-Tripel überträgt.
Betrachtet man eine "farblose" Verteilung der Form
lassen sich weitere Festlegungen treffen, die aus praktischen Gründen in die endgültige Definition der CIE 1931 rgb-Farbkurven einfließen. Dabei ist Φ0 wieder die Leistung und [λmin,λmax] der Empfindlichkeitsbereich des menschlichen Auges. Verteilungen dieser Form verursachen einen weißen bzw. grauen Eindruck unterschiedlicher Intensität, abhängig von Φ0. Für Φe(λ) in die obige Definition der RGB-Werte einsetzen liefert
Damit für farblose Verteilungen die R-, G- und B-Werte gleich sind, reskaliert man nun ρ(λ), ϒ(λ) und β(λ) derart, dass
die entsprechend reskalierten Funktionen sind. Bleibt allerdings die Frage, welcher Wert das sein soll, auf den die drei Integrale getrimmt werden sollen. Dazu schlug man 1931 eine Brücke zur photopischen Hellempfindlichkeitsfunktion V(λ): eine geeignet gewichtete Summe der geeignet skalierten rgb-Werte sollte V(λ), also im Wesentlichen die wahrgenommene Helligkeit (perceived brightness) für jedes Licht ergeben. Um 1930 dachte man nämlich, dass die wahrgenommene Helligkeit ident mit Leuchtdichte(Luminaz, luminance) ist und sich so linear bei Farbmischung verhält, was nicht ganz richtig ist (→ Helmholtz-Kohlrausch-Effekt - je "näher" eine Farbe der Spektralfarbe kommt, desto heller wirkt sie, Bezold-Brücke-Phänomen, Hunt-Effekt). In Wahrheit wird also so "nur" die Luminanz, die zwar die frequenzabhängige Empfindlichkeit des Auges berücksichtigt, sich aber von der subjektiv wahrgenommenen Helligkeit unterscheidet, einbezogen. 1931 allerdings, durch die unkorrekte Vermutung motiviert (die übrigens für punktförmige Lichtquellen durchaus richtig ist), hatte man mittles V(λ) die Gewichtungsfaktoren in der Summe der rgb-Werte - die sog. Luminanzkoeffizienten, der Anteil der rgb-Empfindlichkeitkurven an der Hellempfindlichkeit - und die notwendige Skalierung der rgb-Basisfunktionen folgendermaßen bestimmt:
wobei a1, a2 und a3 die Luminanzkoeffizienten bezeichnen. Mit der Skalierung
folgt a1=1. Anschließend bestimmt man mittels der Methode der kleinsten Quadrate die beiden anderen Koeffizienten zu a2=4.5907 und a3=0.0601. Das ist notwendig, da keine Linearkombination der rgb-Farbkurven exakt V(λ) liefert.
Bildet man nun
erhält man
Damit kann man nun zusammenfassend folgende Definition geben:
Jeder durch eine spektrale Verteilung Φe(λ) hervorgerufene Farbeindruck wird im CIE 1931 RGB-Farbmodell durch das Tripel
beschrieben, wobei die rgb-Kurven durch oben beschriebene Messung und anschließender Reskalierung bestimmt werden, sodass gilt:
V(λ) wird dabei durch das Flimmerprinzip experimentell bestimmt. R+4.5907G+0.0601B ist proprtional zur Luminanz (summiere die Integrale und vergleiche mit der Definition von Luminanz!).
Der Hilbertraum der Spektralverteilungen kolabiert also zu einem 3-dimensionalen rellen Vektorraum (der CIE-"Farbraum"/das CIE-Farbsystem) mit der Basis
oft auch als CIE RGB-Farbraum bezeichnet. Alle Spektalverteilungen, die den gleichen Farbeindruck verursachen, sind zu einem Punkt zusammengefallen. Da die angegebene rgb-Basis übrigens ja in keiner Weise ausgezeichnet ist, kann man auch andere Basen wählen, und genau das werden wir weiter unten tun.
Als letzter Streich kann jetzt noch die Normfarbtafel gewonnen werden: man bilde
Es gilt natürlich
und daher kann jede Farbe, bezogen auf Normintensität - also die Farbart, wenn man so möchte - in einem zweidimensionalen Diagramm mit r als Abszisse und b als Ordinate eingetragen werden, s. Abb.2.
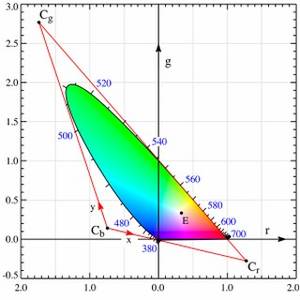
- Abb. 2: CIE rg-Normfarbtafel - Spektralfarbenkurve & Purpurgerade, Unbuntpunkt E, eigezeichnet ist auch das einhüllende Dreieck, das zur Basis in der CIE xy-Normfarbtafel wird. Die Farben sollte man nicht zu ernst nehmen, da bisher kein Monitor der Welt alle Farben des CIE-Systems darstellen kann. (Quelle: Wikipedia)
Der CIE 1931 XYZ-Farbraum
Wie angekündigt wählen wir nun eine andere Basis im CIE-Farbsystem und damit neue Koordinaten, mit X,Y und Z bezeichnet. Wieder sei x=X/(X+Y+Z), y=Y/(X+Y+Z), z=Z/(X+Y+Z). Die Motivation für den Übergang zu anderen Koordinaten bestand hauptsächlich darin, Berechnungen zu vereinfachen (1931 waren solche Berechnungen Handarbeit). Dabei wurde folgendes verlangt:
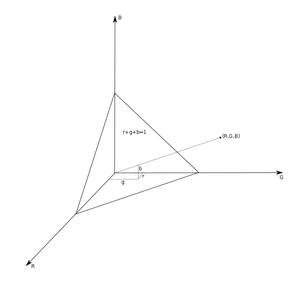
- Die Farbkoordinaten der sichtbaren Farben sollten in der neuen Basis alle positiv sein, auch wenn den neuen "Primärfarben" (die Basisvektoren) keine tatsächlich sichtbaren Farben entsprechen. In Abb. 3 bedeutet das, CbCr und CbCg als Basis im Chromazitätsdiagramm zu wählen und damit das rot umrandete Dreieck in den 1. Quadranten im xy-Chromatizitätsdiagramm zu befördern.
- Eine der neuen Basisfunktionen sollte die 1924-Hellempfindlichkeitskurve V(λ) sein (eine Idee von Erwin Schrödinger), da dann die wahrgenomme Helligkeit (perceived brightness) direkt an einer Koordinate ablesbar wäre und nicht mehr über die Luminanzkoeff. wie oben berechnet werden müssen. Das stimmt natürlich nicht ganz, da sich mit V(λ) die Luminanz und nicht die wahrgenommene Helligkeit ergibt, die nicht ident sind, s. weiter oben! Heute würde man darauf also wahrscheinlich verzichten.
- Für "farblose" Verteilungen sollte auch für die neuen Koordinaten wieder gelten X=Y=Z, also insbesonders x=y=z=1/3, siehe Abb.2, "Unbuntpunkt" E.
- In Abb. 2 sieht man, dass ab ca. 650nm die Spektralfarbenkurve fast mit der Geraden r+g=1 zusammenfällt. Das liegt an der Wahl der roten Primärfarbe bei 700nm: die blauen Anteile verschwinden ab Wellenlängen um 650nm annähernd, also b=0. Tatsächlich allerdings liegt die Linie r+g=1 ein wenig innerhalb der Spektralfarbenkurve, da die blaue Hellempfindlichkeitskurve zw. der blauen Primärfarbe und 670nm kleine negative Werte aufweist. Wie auch immer: wird die Gerade CgCr so gewählt, dass möglichst viele Punkte der Spektralfarbenkurve auf ihr liegen, dann gilt in der neuen Basis für möglichst viele Spektralfarben x+y=1 (das entspricht im xy-Chromatizitätsdiagramm jener Geraden, die Cr=(1,0) und Cg=(0,1) enthält), also z=0 (wegen x+y+z=1) also für möglichst viele λ die z-Basisfunktion null (es sind ja Spektralfarben!).
Das lässt sich folgendermaßen formalisieren:
Sei C der 3-dimensionale reelle Vektorraum des CIE-Farbsystems. Gesucht ist die Matrixdarstellung Tik der nichtsingulären Transformation (genauer müsste es heißen: T ist die Matrixdarstellung MB',B (idC) der Identität auf C, aber The Stophoto will hier nicht lineare Algebra betreiben):
Die Komponenten einer Farbe ergeben sich in der neuen Basis dann zu
wobei das hochgestellte T transponieren bedeutet. Aus den obigen Bedingungen erhält man die Koeffizienten der Matrizen nun schrittweise wie folgt:
Zwecks Inkorporation von V(λ) als Basiselement verwendet man die weiter oben durch Festlegung erzeugte Eigenschaft, dass R+4.5907G+0.0601B und damit auch r+4.5907g+0.0601b proportinal zur Luminanz ist (die seltsamen Zahlen sind die durch die Methode der kleinsten Quadrate gewonnenen Luminanzkoeffizienten, s. oben). Die Punkte mit keiner Luminanz liegen dann auf der Geraden r+4.5907g + 0.0601(1-r-g)=0 bzw. 0.9399r+4.5306g+0.0601=0 (*), der sog. Alychne CbCr (von gr. lychnos = Licht,Lampe). Soll nun ein neues Basiselement mit V(λ) ident sein - sagen wir die Y-Basis (0,1,0) -, dann muss die Alychne alle Punkte mit Y=0 enthalten, insbesonders die beiden anderen Basiselemente (1,0,0) und (0,0,1) (in XYZ-Komponenten). Die r,g-Koordinaten der beiden X,Z-Basisvektoren müssen also die Gleichung (*) erfüllen!
Als nächstes nutzt man die oben beschriebene Beobachtung, dass die Spektralfarbenkurve bei hohen Wellenlängen (>650nm) fast linear verläuft. Eine Analyse der Daten ergibt, dass der Abschnitt mit hinreichender Genauigkeit in der Geraden g = -100/99(1+r) (**) enthalten ist und andererseits diese Gerade nirgends innerhalb der Spektralkurve liegt (Positivität ist das Ziel!).
Lösen von (*) und (**) liefert die rg-Koordinaten von Cr(1.2749, -0.2777) und weiter b=0.0028. Durch Wahl von Cg(-1.74,2.7677), b=-0.0277 und Cb(-0.7430,0.1408), b=1.6022 radiert die Verbindung CgCb dann knapp am Punkt der Spektralfarbenkurve mit kleinstem r vorbei (die gewählte Gerade hat die Gleichung 2.6268r+0.9979g=-1.8113).
Bedenkt man, dass die rgb-Koordinaten von Cr,Cg und Cb in der Ebene R+G+B=1 liegen und die XYZ-Einheitsvektoren daher irgendwo beliebig auf einer Geraden vom Ursprung durch Cr,Cg bzw. Cb, ist klar, dass diese durch das bisherige nur bis auf Skalierungsfaktoren bestimmt sind (s. Abb. 3):
Daraus erhält man T und (TT)-1:
Es bleibt noch α,β und ϒ zu bestimmen. Dazu zieht man die verbleibende Forderung heran, dass nämlich die Koordinaten des Unbuntpunkts E im neuen Chromatizitätsdiagramm analog bei x=y=z=1/3 liegen sollen. Aus
bekommt man α=1.85481, β=0.5154, ϒ=0.6298 und damit für die endgültige Transfomationsmatrix:
Bleibt erstens noch zu bemerken, dass 1931 kleine Korrekturen an den Werten vorgenommen wurden, um die Y-Basisfunktion ident mit V(λ) zu bekommen (unsere Alychne-Gleichung basiert auf Näherung durch die Methode der kleinsten Quadrate). Und zweitens implizieren unsere Festlegungen
Zu Farbsehen, Photometrie und Strahlung, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile
Referenzen:
- Wright, William David (1928). "A re-determination of the trichromatic coefficients of the spectral colours". Transactions of the Optical Society 30 (4): 141–164. DOI:10.1088/1475-4878/30/4/301.
- Guild, John (1931). "The colorimetric properties of the spectrum". Philosophical Transactions of the Royal Society of London (Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, Vol. 230) A230: 149–187. JSTOR 91229.
- Fairman, H. S., Brill, M. H. and Hemmendinger, H. (1997), How the CIE 1931 color-matching functions were derived from Wright-Guild data. Color Res. Appl., 22: 11–23. doi: 10.1002/(SICI)1520-6378(199702)22:1<11::AID-COL4>3.0.CO;2-7.
- Gernot Hoffman, CIE Color Space, www.fho-emden.de/~hoffmann/ciexyz29082000.pdf

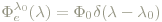
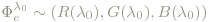
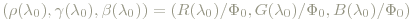
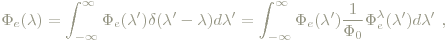
![\Phi_e \sim \left[ \begin{array}{c} \int_{-\infty}^{\infty}\Phi_e(\lambda)\rho(\lambda)d\lambda \\ \int_{-\infty}^{\infty}\Phi_e(\lambda)\gamma(\lambda)d\lambda \\ \int_{-\infty}^{\infty}\Phi_e(\lambda)\beta(\lambda)d\lambda \end{array}\right] =: \left[ \begin{array}{c} R(\Phi_e)\\ G(\Phi_e) \\ B(\Phi_e)\end{array}\right]](typo3temp/math/0fac7c1fa0056a12eb5fefef7d855415.png)
![\Phi_e^1\oplus\Phi_e^2 \sim
\left[\begin{array}{c}
\int_{-\infty}^{\infty}(\Phi_e^1(\lambda)+
\Phi_e^2(\lambda))\rho(\lambda)d\lambda \\ \int_{-\infty}^{\infty}(\Phi_e^1(\lambda)+
\Phi_e^2(\lambda))\gamma(\lambda)d\lambda \\ \int_{-\infty}^{\infty}(\Phi_e^1(\lambda)+
\Phi_e^2(\lambda))\beta(\lambda)d\lambda
\end{array}\right] =
\left[\begin{array}{c}
R(\Phi_e^1) \\ G(\Phi_e^1) \\ B(\Phi_e^1)
\end{array}\right] +
\left[\begin{array}{c}
R(\Phi_e^2) \\ G(\Phi_e^2) \\ B(\Phi_e^2)\end{array}
\right]](typo3temp/math/0a206b230d6b611a7b548913a5356ddc.png)
![\Phi_e^{const}(\lambda) = \left\lbrace \begin{array}{cl} \frac{\Phi_0}{\lambda_{max}-\lambda_{min}} & \text{ wenn } \lambda \in [\lambda_{min},\lambda_{max}] \\0 & \text{ sonst } \end{array}](typo3temp/math/e16b84d8ccee3dd4e034583e8b16edc7.png)
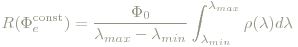
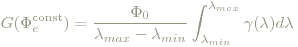
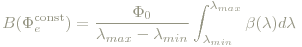
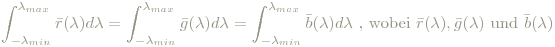
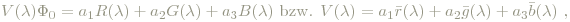
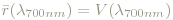
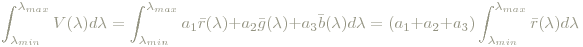
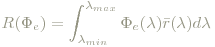
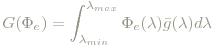
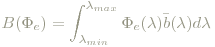
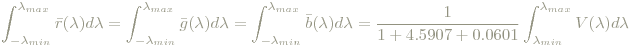

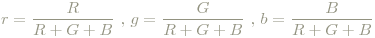
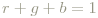
![\mathbf{T}:B=\left[
\begin{array}{c}
\bar{r}\\ \bar{g}\\ \bar{b}
\end{array}
\right]
\rightarrow
B'=\left[
\begin{array}{c}
\bar{x}\\ \bar{y}\\ \bar{z}
\end{array}
\right]
= \mathbf{T}\cdot
\left[
\begin{array}{c}
\bar{r}\\ \bar{g}\\ \bar{b}
\end{array}
\right]](typo3temp/math/d7485329405ec8f9aa77e8f04ac81c66.png)
![\left[
\begin{array}{c}
X\\ Y\\ Z
\end{array}
\right]
= (\mathbf{T}^T)^{-1}\cdot
\left[
\begin{array}{c}
R\\ G\\ B
\end{array}
\right]\trextrm{ , }](typo3temp/math/08b39ed1b2e2cb6f267343aca6f586ac.png)
![\bar{x}=\alpha \left[ \begin{array}{c} 1.2749 \\ -0.2777 \\ 0.0028 \end{array}\right]=\mathbf{T}\left[ \begin{array}{c} 1\\ 0\\ 0\end{array} \right]\textrm{ , } \bar{y}=\beta \left[ \begin{array}{c} -1.74 \\ 2.7677 \\ -0.0277\end{array} \right]=\mathbf{T}\left[ \begin{array}{c} 0\\ 1\\ 0\end{array} \right] \textrm{ und } \bar{z} = \gamma \left[ \begin{array}{c} -0.7430 \\ 0.1408 \\0.1408 \end{array} \right]=\mathbf{T}\left[ \begin{array}{c} 0\\ 0\\ 1\end{array} \right]](typo3temp/math/03835bf1637518956b59e877821a1d25.png)
![\mathbf{T}=\left[\begin{array}{ccc} 1.2749\alpha & -0.2777\alpha & 0.0028\alpha \\ -1.74\beta & 2.7677\beta & -0.0277\beta \\ -0.7430\gamma & 0.1408\gamma & 1.6022\gamma\end{array}\right]\textrm{ , }(\mathbf{T}^T)^{-1}=\left[\begin{array}{ccc} 0.9088/ \alpha & 0.5751/\alpha & 0.3709/\alpha \\ 0.0912 /\beta & 0.4187 /\beta & 0.0055 /\beta \\ 0.0000 /\gamma & 0.0062 /\gamma & 0.6236 /\gamma\end{array}\right]](typo3temp/math/50a6375a9c0c95d229a005ecf90d1ca0.png)
![\left[\begin{array}{c}1/3\\ 1/3\\ 1/3 \end{array} \right] = \left[\begin{array}{ccc} 0.9088/ \alpha & 0.5751/\alpha & 0.3709/\alpha \\ 0.0912 /\beta & 0.4187 /\beta & 0.0055 /\beta \\ 0.0000 /\gamma & 0.0062 /\gamma & 0.6236 /\gamma\end{array}\right]\left[\begin{array}{c}1/3\\ 1/3\\ 1/3 \end{array} \right]](typo3temp/math/546e50047fb247baa66beba072fed49b.png)
![(\mathbf{T}^T)^{-1}=\left[\begin{array}{ccc} 0.4900 & 0.3100 & 0.2000 \\ 0.1769 & 0.8124 & 0.0107 \\ 0.0000 & 0.0099 & 0.9901 \end{array}\right]](typo3temp/math/5c7e63254f7cf16beae649833bb343a8.png)