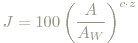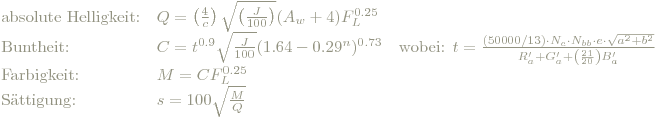Empfindungsgemäße Farbräume, Color Appearance Models
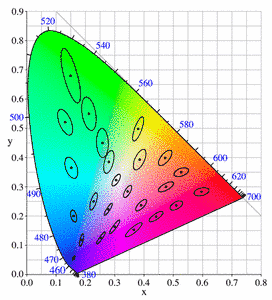
- Abb. 1: McAdam-Ellipsen (Quelle: Wikipedia).
Aus dem CIE-Normvalenzsystem mit seinem umfassenden Farbsystem wurden im Laufe der Zeit durch geeignete Transformationen weitere Farbräume gewonnen, um einen Nachteil des CIE XYZ-Farbraumes wegzubekommen: die Abstände zweier Punkte in XYZ-Koordinaten entsprechen nicht den wahrgenommen Farbunterschieden, oder locker gesagt: wenn zwei Farben A und B die selbe "gefühlte" (wahrgenommene) Differenz wie zwei andere Farben D und E haben, dann würde man wollen, dass ihre (euklidischen) Abstände im Farbraum auch gleich wären − |AB|=|DE|. Im CIE XYZ-Farbraum ist das nicht der Fall!
Vielmehr entsprechen im CIE XYZ-Farbraum jene Farben, die für das Auge ununterscheidbar sind unterschiedlich großen "Knödeln" (Ellipsoide, sog. isodiscrimination contours), abhängig von der Position der Farben im Farbraum. Ihre Projektionen im xy-Chromatizitätsdiagramm sind die McAdam-Ellipsen, s. Abb 1.Die Farbabstandsschwelle ist also unterschiedlich groß.
Um das auszugleichen verzerrt man die Normfarbtafel solange, bis die Ellipsen zu Kreisen werden. Die so gewonnene Farbtafel heißt U(niform)C(olor)S(cale)- Farbtafel, die neuen Koordinaten u',v' (sie reflektieren die von CIE anno 1976 akzeptierte Transformation, die ursprünglichen UCS-Werte sind ein wenig anders) berechnen sich so (dahinter steckt reine Empirik!):
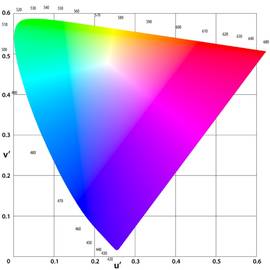
- Abb. 2: UCS 1976 Farbdiagramm (Quelle: Wikipedia).
Das Ergebnis der Transformation ist das Chromatizitätsdiagramm in Abb.2.
Das neue Farbdiagramm gibt nun Anlass zur Suche nach geeigneten Transformationen, die das XYZ-System in ein empfindungsgemäßes Farbsystem überführen. Dabei erfolgt auch gleich die Trennung von Helligkeit und Farbart, um eine unabhängige Kodierung zu ermöglichen. Das erfordert aber zuerst einen adäquaten Begriff für Helligkeit - dazu dient die psychometrische Helligkeitsfunktion L*, die The Stophoto schon unter "Farbsehen" eingeführt hat. Hier nun die genauere Definition der psychometrischen Helligkeitsfunktion, wie sie von CIE 1976 spezifiziert wurde:
Psychometrische Helligkeitsfunktiom nach CIE 1976
Basis der Definition ist die Y-Koordinate aus dem CIE XYZ-Farbraum. Die Y-Basisfunktion wurde ja ident mit der V(λ)-Kurve (der photopischen Hellempfindlichkeit) gesetzt, siehe unter "CIE-Normvalenzsystem". Unter "Photometrie und Strahlung" ist nachzulesen, dass dann die Y-Koordinate wegen folgenden Zusammenhangs proportional zur Leuchtdichte ist:
Also ist Y proportional zur Leuchtdichte (Helligkeit, Luminanz). Darauf basierend wird nun die psychometrische Helligkeitsfunktion folgendermaßen festgelegt:
Dabei ist Yn die Y-Koordinate eines als weiß ausgezeichneten Objekts (des Weißpunktes, was "Weiß" ist hängt ja von der Beleuchtung (Illumination) ab), und der Wertebereich wird auf das Intervall [0;1] beschränkt. Sie definiert den Begriff relative Helligkeit (lightness) konform mit der unter "Farbsehen" gegebene Festlegung als das Verhätnis von Helligkeit (brightness) zur Helligkeit(brightness) von Weiß. Unter Helligkeit (brightness) wird dabei die photometrische Helligkeit Y verstanden.
Mit der Einbeziehung des Weißpunktes geschieht ein erster entscheidender Schritt hin zu Farberscheinungsmodellen: während man im CIE-Normvalenzsystem Farben nur für eine normierte Beobachtungssituation angeben kann, ist mit der Berücksichtigung eines Referenzweiß bei Kenntnis der Beleuchtungssituation (Illumination) möglich, Vorhersagen über die Farbwirkung bei unterschiedlichen Bedingungen zu machen!
Relativer Farbraum, Normlicht, Weißpunkt, Color Adaption Model
Es begegnet uns also erstmals eine "relative" Größe, L*. Reproduktion von Farben ist unter Angabe des Referenzweiß (das oft impliziert wird) möglich! Die Koordinaten des Referenzweiß bzw. Weißpunktes sind nichts anderes als die Farbkoordinaten des verwendeten Beleuchtungslichts (illuminant) im jeweiligen Farbsystem. Standardisierte Referenzweiß (standard illuminants) sind z.B. ein schwarzer Strahler bei 2856K (Illuminant A), D50 und D65 (gemittelte Tageslichtspektren - Europa, Mittag), u.a. Mit der Angabe vom Referenzweiß kann durch unterschiedliche Beleuchtung notwendige Farbkorrektur in den Farbräumen erfolgen. Verursacht werden die notwendigen Anpassungen durch Eigenschaften des Sehapparates wie bspw. die Hellanpassung (light adaption), die Dunkelanpassung (dark adapation) und - ganz eintscheidend - die Farbanpassung (chromatic adaption).
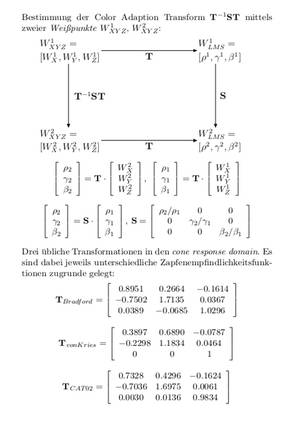
Die Berechnungen zur chromatischen Adaption erfolgen dabei in Farbräumen, deren Basis aus zu den Zapfenempfindlichkeitsfunktionen ähnlichen Funktionen besteht. Die Grundidee ist nämlich, dass die Farbanpasssung des Auges durch jeweils unterschiedliche, von Umgebung und zeitlichem Verlauf abhängige Verhältnisse der Zapfenempfindlichkeiten modelliert werden kann. In den "Zapfen"-Farbräumen (cone response domains) ist die chromatische Adaption dann durch eine diagonale Matrix beschreibbar, man spricht von einem C(olor) A(daption) M(odel) bzw. einer C(olor) A(daption) T(ransform), s. Abb.3. Im CIECAM02, das The Stophoto weiter unten noch genauer beschreibt, kommt eine von Kries-Transformation zum Einsatz (CAT02).
Mit diesem Wissen ausgerüstet geben wir nun zwei Transformationen an, die zu "empfindungsgemäßen" relativen Farbräumen führen (CIE RGB/XYZ waren einerseits absolut und andererseits nicht empfindungsgemäß!). Dabei wird eine implizite Farbanpassung durch die Berücksichtigung der Luminanz des Weißpunktes durch die relativen Helligkeit vorgenommen.
Der CIE LUV 1976-Farbraum (L*u*v*)
Zwei der neuen Farbkoordinaten - u* und v* - sollen hier proportional zu u' bzw. v' sein, um die Farbabstandsgleichheit zu gewährleisten, als dritte Koordinate wird die psychometrische Helligkeitsfunktion L* gewählt. Ebenen mit konstantem L* werden Farbartebenen genannt. Die Transformationsformeln vom XYZ- ins L*u*v*-System sind:
Dabei sind un' und vn' die Koordinaten des Unbuntpunktes aus Abb. 2. Darauf aufbauend lassen sich nun weitere Größen festlegen. Ihre Definitionen sind fast wörtlich aus "Bergman/Schaefer, Lehrbuch der Experimental Physik, Band 3, Optik" entnommen.
- psychometrische Buntheit (Chroma) − sie ist der Abstand einer Farbe zum Unbuntpunkt, bzw. ein wenig freier: sie beschreibt, wie stark sich ein Farbeindruck von einem unbunten Eindruck gleicher Helligkeit unterscheidet:
- psychometrische Sättigung − sie beschreibt, wie stark sich ein Farbeindruck von einem unbunten Eindruck unabhängig von der Helligkeit unterscheidet:
- Farbtonwinkel, Fabton, Buntton (hue) − er beschreibt, wie Farbwahrnehmung durch Bezeichnungen wie "rot'', "grün'', "violett'', "gelb'' usw. voneinander unterschieden werden. Genauer gesagt, ist er der Winkel zwischen u* und v* in der Farbartebene (man bedenke bei der Veranschaulichung, dass der Weißpunkt in den *-Koordinaten im Ursprung sitzt!):
- Farbabstand − er ist der euklidische Abstand zweier Farben:
Bei ΔE*uv =1 spricht man von "gerade noch wahrnehmbarer Differenz".
- Farbtondifferenz − sie ist die totale Farbdifferenz, abzüglich der Unterschiede in Buntheit und Helligkeit:
Genauer gibt sie den sagen wir mal "euklidischen Linienelementanteil" der Hue-Komponente an, vergleiche dazu das Linienelement in ZylinderKoordinaten: ΔE*uv2 = ΔC*uv2 + C*uv2Δhuv2 + ΔL*2 (ds2=dr2+r2dφ2+dz2, tatsächlich entspricht C*uv dem Radius und huv dem Winkel).
Der CIE LAB 1976-Farbraum (L*a*b*)
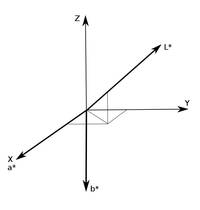
Die Transformation in die CIE LAB-Farbkoordinaten führt zu einer besseren empfindungsgemäßen Gleichabständigkeit als bei CIE LUV. Zudem hat das CIE LAB-System die Eigenschaft, das Gegenfarbenmodell sichtbar zu machen: die Gegenfarben Rot und Grün kommen auf der a*-, die Gegenfarben Blau und Gelb auf der b*-Achse jeweils gegenüber zu liegen. Auf der L*-Achse werden wieder wie vorher die psychometrischen Helligkeitsfunktionswerte aufgetragen. Um die bessere Erfassung der Empfindungsmäßigkeit zu erreichen, werden die Transformationsformeln von CIE XYZ zu L*a*b* ein bisschen unansehnlicher:
Für kleine Werte von C/Cn (soll heißen X/Xn, Y/Yn bzw. Z/Zn jeweils kleiner als 6/29) ist die dritte Wurzel durch 1/3⋅(29/6)2⋅(C/Cn)+4/29 zu ersetzen. Xn,Yn und Zn bedeuten wieder die Weißpunktkoordinaten in CIE XYZ.
Die Schritte der Konversion von XYZ nach L*a*b* (eine evt. Farbanpassung sei schon durchgeführt) in Kurzform: Weißpunktanpassung (Division durch Normweißwerte), (nichtlineare) Entzerrung der so erhaltenen relativen X-, Y, und Z-Werte (vermöge der dritten Wurzel), lineare Achsentransformation und abschließende Skalierung (die Overall-Faktoren). Die Beschaffenheit der Achsentransformation ist dabei in Abb. 4 dargestellt. Die L*-Achse entspricht den Werten mit X=Y=Z (die Unbuntgerade), X und a* fallen zusammen und b zeigt in Richtungen negativen Z's.
Da sich kein leuchtdichte- bzw. helligkeitsunabhängiger Quotient mehr bilden lässt, existiert im CIE LAB keine zu früher vergleichbare Farbtafel!
Analog zu CIE LUV lassen sich wieder Buntheit (Chroma) und Farbton (Hue) definieren (Helligkeit ist ident mit oben):
Da sich wie erwähnt kein helligkeitsunabhängiger Quotient bilden lässt, wird die zu L*u*v* analoge Definition der Sättigung allerdings durch die folgende, die mit der unter "Farbsehen" gegebenen Definition verträglich ist, ersetzt:
Sowohl das L*u*v*− als auch insbesonders das L*a*b*−System sind mehr als bloße Farbräume (also eine Menge von Valenztripel mit Koordinatensystem), denn:
- Sie definieren wichtige perzeptive Größen, wie Helligkeit (lightness), Buntheit und Sättigung.
- Sie sind "empfindungsgemäß" bezüglich des Farbabstandes (wegen der dritten Wurzel und den Skalierungen).
- Sie berücksichtigen Referenzweiß (wegen X/Xn, Y/Yn, Z/Zn), ermöglichen also chromatische Adaption.
L*u*v* und L*a*b* können damit als Color Appearance Model (CAM) (Farberscheinungsmodell) bezeichnet werden. Allerdings berücksichtigt keines von beiden Dinge wie Änderungen von Farbhintergrund, Umgebung, Luminanz u.ä.. Begriffe wie Helligkeit (im Sinne von brightness) und Farbigkeit (colorfulness) sind bei beiden nicht enthalten. Es ginge also besser, und eine solche Verbesserung ist das CIECAM02, das aktuellste CAM der Commission internationale de l'éclairage. The Stophoto möchte es zum Schluss dieses Abschnitts kurz vorstellen.
Color Appearance Model, CIECAM02
Ziel eines brauchbaren Color Appearance Models ist die Inkorperierung einer adäquaten CAT, Berücksichtigung von Luminanz- und Umgebungsabhängigkeiten der Farbwahrnehmung sowie diverser Farbeffekte (Farbkonstanz, Hunt-Effekt, Stevens-Effekt, Helmholtz-Kohlrausch-Effekt), und Bestimmung der wahrnehmungsrelevanten Größen wie Chroma, Sättigung, Helligkeit (brightness), relativer Helligkeit (lightness), und Farbigkeit. CIECAM02 ist ein hinsichtlich dieser Kriterien geeignetes CAM, basierend auf CIECAM97s ("s" für simplified, auch ein CIECAM97c − "c" für comprehensiv − war vorgesehen, existiert aber nicht). Zweck des Ganzen ist die wahrnehmungsgetreue Kodierung von Farben, um Vergleichbarkeit und ihre möglichst genaue Reproduktion zu ermöglichen.
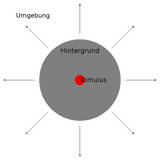
Abb. 5 zeigt die im CIECAM02 herangezogenen Bereiche zur empfindungsgemäßen Bewertung eines Farbreizes: der Bereich mit dem eigentlichen Stimulus, der Hintergrundbereich und die Umgebung. Der Stimulusbereich entspricht dem 2°-Sichtfeld des CIE-Normalbeobachters, die Umgebung einem 10°-Sichtfeld. Hintergrundbereich und Umgebung gemeinsam wird als adaptives Feld bezeichnet. Diese Festlegungen können ggf. den Erfordernissen angepasst werden, bspw. bei digitalen Bildern: der Stimulusbereich entspricht dort einem Pixel, die Umgebungshelligkeit der eines neutralen Grauton (gemittelt über die Helligkeit der Bildfarben), womit das Ganze auch skalierungsunabhängig wird.
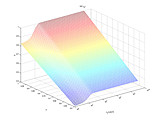
- Abb. 6: Adaptionsgrad D(F,La). Zum Vergrößern anklicken! (Quelle: Wikipedia)
Im Weiteren werden folgende Größen bestimmt:
- die relativen Tristimulus-Werte X,Y,Z des zentralen Stimulus (die relativen Tristimulus-Werte stammen dabei aus der Umkehrung X=Y/y⋅x, Z=Y/y⋅(1-x-y), wobei Y nach Messung zwischen 0 (perfektes Schwarz) und 100 (perfekt diffuser Reflektor) zu liegen kommt).
- die relativen Tristimulus-Werte Xw,Yw,Zw von Weiß unter den gleichen Bedingungen.
- die relative Luminanz Yb des Hintergrunds.
- die absolute Helligkeit (Luminanz) La des adaptiven Feldes.
Zusätzlich werden durch die Umgebung 3 Parameter im Modell, F (Adaptionsgrad) , c (Umgebungsauswirkung) und Nc (chromatischer Induktionsfaktor), festgelegt. Bei der Zuordnung hilft die Größe Ys=relative Umgebungsluminanz, basierend darauf, dass "Dämmrigkeit" vorliegt, wenn die absolute Helligkeit der Umgebung bei 20% der absoluten Gesamthelligkeit liegt (gray world assumption):
- Dunkle Umgebung (bspw. ein Projektor in einem dunkeln Raum): c=0.525, F=0.8, Nc=0.8, Ys=0.
- Dämmrige Umgebung (bspw. beim Fernsehabend): c=0.59, F=0.9, Nc=0.95, 0<Ys<0.2.
- "Durchschnittliche" Umgebung (bspw. Betrachtung von Oberflächenfarben von Objekten): c=0.69, F=1, Nc=1, YS≥0.2.
- Für dazwischenliegende Bedingungen kann linear interpoliert werden.
Sodann kommt es zur chromatischen Adaption (CATCIE02): zuerst erfolgt eine Transformation in einen LMS-Raum (Li et al-Farbraum), wo die L- und S-Basiskurven gegenüber den tatsächlichen Zapfenempfindlichkeiten schmäler sind (spectral sharpening). Für die Transformationsmatrix s. Abb. 3. Dann wird der Adaptionsgrad (des Auges) D(F,La) (discounting) festgestellt (s. auch Abb.6):
Für ein selbstleuchtendes Medium wird D=1 gesetzt, keine Adaption bedeutet D=0. Dann erfolgt die Weißpunktanpassung durch Multiplikation mit:
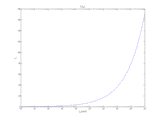
- Abb.7: FL Faktor. Zum Vergrößern anklicken! (Quelle: Wikipedia).
Der Index W bezieht sich auf den Weißpunkt unter dem Test-, der Index WR auf den Weißpunkt unter dem Referenzlicht. Wird das Referenzlicht mit LWR=MWR=SWR (equal energy illuminant, der Standard für CIECAM02) und das Referenzweiß als perfekter diffuser Reflektor (YWR=100) angenommen, reduzieren sich die Faktoren vor D auf YW/LW, YW/MW und YW/SW. Das Ergebnis der Transformation sei [L' M' S']T.
Nun erfolgt die sogenannte Nachadaption zwecks Berücksichtigung des Hunt- und des Stevens-Effekts. Dazu wird zuerst in den Hunt-Pointer-Estevez-Farbraum (HPE) transformiert. Davor wird noch rücktransformiert: [X Y Z]T = MCAT-1 [L' M' S']T − also zurück von "Li et al" nach CIE XYZ. Man bekommt dann die neuen Tripel mit [R' G' B']T = MH [X Y Z]T, wobei die Transformationsmatrix von XYZ nach HPE lautet:
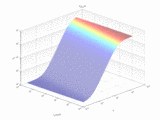
- Abb. 8: Kompressions- antwortfunktion für L-(R-)Werte. Zum Vergrößern anklicken! (Quelle: Wikipedia).
Warum ein erneuter Farbraumwechsel? Dazu ein Zitat aus "Nathan Moroney, Mark D. Fairchild, Robert W. G. Hunt, Changjun Li, M. Ronnier Luo, and Todd Newman. The CIECAM02 color appearance model." (s. Referenzen):
CIECAM02, like CIECAM97s, makes use of one space for the chromatic adaptation transform and another for computing perceptual attribute correlates. This adds complexity to the model but pending additional research, it would appear that chromatic adaptation results are best predicted in a space that has some degree of sharpening. The nature and degree of this sharpening is still subject to debate but it should be noted that CAT02 does incorporate some degree of sharpening. In comparison the use of a space closer to the cone fundamentals, such as the Hunt-Pointer-Estevez or Stockman-Sharpe fundamentals, provides better predictions of perceptual attribute correlates.
Damit noch nicht genug: es erfolgt die Anwendung der sogenannten Kompressionsantwortfunktion, die wieder physiologische Umstände berücksichtigt (siehe dazu R.W.G. Hunt, C. J. Li and M. R. Luo, “Dynamic cone response functions for models of color appearance”, Color Res. Appl.). Sie ist
wobei C'a bzw. C' für den jeweiligen Tristimuluswert R', G',B' bzw. R'a, G'a, B'a in HPE stehen. FL ist der sogenannte luminance-level adaption factor, siehe. Abb. 7 und Abb. 8:
Nach all der Berücksichtigerei diverser Effekte und physiologischer Eigenheiten im Rahmen der Nachbildung der Farbanpassung des menschlichen Sehens − alles letztlich basierend auf experimentell gefundenen Daten und Interpolationen − werden die gewonnen Werte von R'a, G'a und B'a zur Definition von mit der Wahrnehmung eng verknüpften Größen herangezogen, die sich den zunächst intuitiven Begriffen der Farbwahrnehmung sehr gut annähern und prediktive Aussagekraft besitzen. Hier fließt die relative Luminanz des Hintergrundes entscheidend ein (verschiedene Kontraste haben wesentlichen Einfluß auf die subjektive Farbwahrnehmung).
CIECAM02 definiert Entsprechungen für die Oponenten Gelb-Blau, Rot-Grün (siehe dazu die Bemerkung zum Gegenfarbenmodell) usw. folgendermaßen:
wobei die Rot-Grün-Entsprechung die Größe der Abweichung von C1 von der Bedingung für reines Gelb (C1 = C2 / 11) und die Gelb-Blau-Entsprechung die mittlere Abweichung von C1 von eindeutigem Rot- (C1 = C2) und eindeutigem Grünempfinden (C1 = C3) ist (der Faktor 1/4.5 berücksichtigt, dass das menschliche Auge weniger Zapfen im blauen Bereich hat, dort also weniger empfindlich reagiert, die Bedingungen sind empirisch ermittelt):
Damit bekommt man "cartesoide" Koordinaten a,b und der Buntton (hue) ist dann analog zu früher als Winkel zwischen a und b definiert:
Da die a,b-Koordinaten der reinen Farbtöne nicht auf einem Kreis um (a,b)=(0,0) liegen, kann man für sie (namentlich Rot, Gelb, Grün und Blau) Exzentrizitäten angeben, die nach Rechnung zwischen 0.7 und 1.2 zu liegen kommen. Damit wird die (a,b)-Ebene winkelabhänig gestreckt/gestaucht, was ausdrückt, dass die Stärke der Farbigkeit vom Farbton abhängt. Zusätzlich wird den reinen Farben die Zahl H, die Bunttonquadratur, mehr oder weniger willkürlich (Nummer x 100) zugeordnet:
Um nun die Werte e und H für beliebige Farbtöne zu bekommen wird linear interpoliert:
wobei die mit 1 und 2 indizierten Werte die jeweils unteren und oberen Nachbarn aus der obigen Tabelle bedeuten.
Eine weitere Größe ist die achromatische Antwort A (achromatic response). Sie ist die "unbunte" Koordinate, analog zu a und b.
Dabei ist der Wert -0.305 der bei Schwarz vorhandene Rauschterm (er wird so gewählt, dass A=0 wenn Y=0). Nbb ist der achromatische Induktionsfaktor, der angibt, wie stark der Hintergrund sich auf die Stimuluswahrnehmung auswirkt (bei 20%-grauem Hintergrund ist Nbb=1), die Größe z=1.48+n1/2 gibt den gleichen Sachverhalt wieder, und beides ist durch empirische Daten gewonnen. Da drinnen steckt via n der Einfluss der relativen Luminanz des Hintergrunds Yb.
Mit A für den Stimulus als auch für den Weißpunkt (AW) definiert man die relative Helligkeit (lightness) J:
Dabei ist c weiter oben durch die Umgebung (dunkel, dämmrig, etc., impact of surround) und z durch den unmittelbaren Hintergrund (zur Berücksichtigung des Simultankontrastes) bestimmt. Die relative Helligkeit wird damit bspw. bei hellem Hintergrund ("großer" Exponent) für niedrige Werte (die achromatische Antwort des Stimulus ist klein im Vergleich zu Weiß) gedrückt (der Stimulus wirkt "noch ein wenig weniger hell"), für sehr helle Stimuli hingegen gehoben - alles wieder unter den div. Voraussetzungen durch das Experiment bestätigt.
The Stophoto gibt hier noch die Formeln für die absoute Helligkeit Q (brightness), die Buntheit C (chroma), die Farbigkeit M (colorfullness) und die Sättigung s an. Die mit diesen Formeln bestimmten Werte für die unter "Farbsehen" definierten Begriffe stimmen gut mit unserer Erfahrung überein - kein Wunder, sind die Formeln ja genau deshalb so konstruiert.
Referenzen:
- Bergmann, Schaefer: Lehrbuch der Experimental Physik, Band 3, Optik. Walter deGruyter, Berlin 2004.
- Praktische Farbmessung. TU Darmstadt. Präsentation zur Vorlesung. www.idd.tu-darmstadt.de/media/fachgebiet_idd/studium_und_lehre/vorlesungen_4/praktische_farbmessung/prfm_ss_2010/prfm_03_farbmessung_h.pdf
- Farbwiedergabe in den Medien. TU Darmstadt. Präsentation zur Vorlesung. www.idd.tu-darmstadt.de/media/fachgebiet_idd/studium_und_lehre/vorlesungen_4/farbwiedergabe_in_den_medien/ws_2011_3/FiM_WS1112_07-3_Farbmetrik_V2.pdf
- Dibakar Raj Pant and Ivar Farup. Riemannian formulation and comparison of color difference formulas. Color Research & Application, 37(6):429–440, 2012.
- Satoshi Ohshima,Rika Mochizuki, Jinhui Chao, Reiner Lenz. Color Reproduction Using Riemann Normal Coordinates. Lecture Notes in Computer Science, Volume 5646, 2009, pp 140-149
- S. Bianco and R. Schettini. Two new von Kries based chromatic adaptation transforms found by numerical optimization. Color Research & Application, 35(3):184–192, 2010. Link.
- Nathan Moroney, Mark D. Fairchild, Robert W. G. Hunt, Changjun Li, M. Ronnier Luo, and Todd Newman. The CIECAM02 color appearance model. In IS&T/SID 10 th Color Imaging Conference, page 23–27, 2002. www.polybytes.com/misc/Meet_CIECAM02.pdf.
- Fairchild, Mark D.; Luo, M. R.; Hunt, R. W. G. (August 2000). "A Revision of CIECAM97s for Practical Applications".
- R.W.G. Hunt, C. J. Li and M. R. Luo, “Dynamic cone response functions for models of color appearance”, Color Res. Appl.

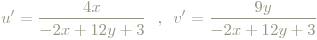
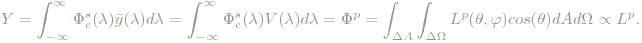
![L^* = 116\cdot \sqrt[3]{\frac{Y}{Y_n}} -16 \textrm{ für } 0.005586<\frac{Y}{Y_n}\leq 1](typo3temp/math/90e8e42f742738fbab0c6c4593e89513.png)
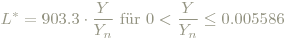
![L^* = 116\cdot \sqrt[3]{\frac{Y}{Y_n}} -16 \textrm{ für } 0.005586<\frac{Y}{Y_n}\leq 1 \textrm{ und } L^* = 903.3\cdot\frac{Y}{Y_n}\textrm{ für } 0 < \frac{Y}{Y_n}\leq 0.005586](typo3temp/math/e9ce9dcdc0d0b9f4f57881beb4b6fb68.png)
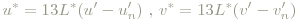
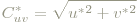
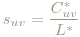

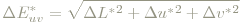
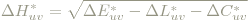
![a^*=500 \left( \sqrt[3]{\frac{X}{X_n}} - \sqrt[3] { \frac{Y}{Y_n}} \right) \textrm{ , } b^*=200 \left( \sqrt[3] {\frac{Y}{Y_n}} - \sqrt[3] {\frac{Z}{Z_n} } \right)](typo3temp/math/8f9a2a01317e1c25aba4e3975ae2b59b.png)
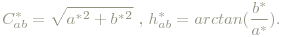
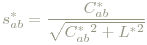
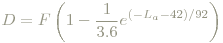
![\left[\begin{array}{ccc}
\frac{Y_W L_{W_R}}{Y_{W_R} L_W}D+1-D & 0 & 0\\
0 & \frac{Y_W M_{W_R}}{Y_{W_R} M_W}D+1-D & 0\\
0 & 0 & \frac{Y_W S_{W_R}}{Y_{W_R} S_W}D+1-D
\end{array}\right]](typo3temp/math/07e34ad46b55077aea24ab35b10901e0.png)
![\mathbf{M}_H=\left[\begin{array}{ccc}
0.38971 & 0.68898 & -0.07868\\
-0.22981 & 1.18340 & 0.04641\\
0 & 0 & 1
\end{array}\right].](typo3temp/math/95756416b35d707ba3aa91fb3f95242e.png)
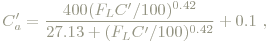
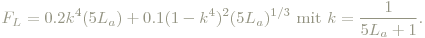
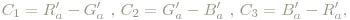
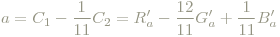
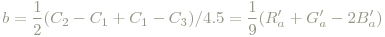
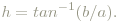
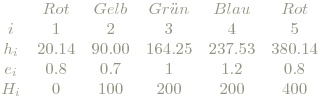
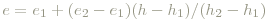

![A=\left[2R'_a+G'_a+ \frac{1}{20}B'_a-0.305\right]N_{bb}\textrm{ , wobei } N_{bb} = 0.725\left(\frac{1}{n}\right)^{0.2}\textrm{ und }n=\frac{Y_b}{Y_w}](typo3temp/math/ee08a69f43ebf4bcefaf76e089ed126e.png)