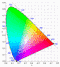
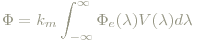Zu Photometrie und Strahlung, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile
Farbsehen
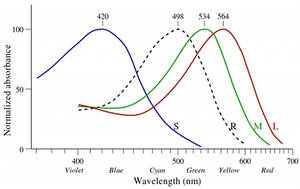
- Abb. 1: spektale Verteilung der Absorbtionsstärke der Zapfen (Quelle: Wikipedia). Zum Vergrößern anklicken!
Farbe ist diejenige Gesichtsempfindung eines dem Auge strukturlos erscheinenden Teiles des Gesichtsfeldes, durch die sich dieser Teil bei einäugiger Beobachtung mit unbewegtem Auge von einem gleichzeitig gesehenen, ebenfalls strukturlosen angrenzenden Bezirk allein unterscheiden kann. (DIN 5033, Blatt 1)
Unsere tagtäglich in fast jedem buchstäblichen Augenblick erlebten Farbeindrücke sind ein innerindividuelles Phänomen, der Begriff "Farbe" ein hoch subjektiver und ganz und gar nicht einfach zu fassender, auch wenn er durch unsere alltägliche Erfahrung trivial erscheint - aber der Leser versuche einmal, einem Blinden die Farbe Rot zu beschreiben! Um zu sinnvollen Begriffen und zu einer objektiven Definition von Farbräumen zu kommen, müssen wir daher zuerst ein bisschen über Farbe (besser: Farbempfindung) und Farbreiz nachdenken.
Dabei bemerkt man, dass der Farbseh-Mechanismus beim Menschen in drei Aspekte zerfällt: einen physikalischen, einen physiologischen und einen psychologisch-neurologischen.
Zuerst zum physikalischen Aspekt: da Farbeindrücke jedenfalls mit Licht zu tun haben, muss Licht irgendeine Eigenschaft besitzen, die Farbwahrnehmung ermöglicht. Diese Eigenschaft ist seine Frequenz bzw. Wellenlänge bzw. Energie (es gelten die Zusammenhänge λ=c/ν, E=hν, wobei c,λ,ν ... Lichtgeschwindigkeit, Wellenlänge, Frequenz, E...Energie, h...Plancksches Wirkungsquantum). Licht ist ja bekanntermaßen eine elektomagnetische Welle (oder doch ein Teilchen... naja, lassen wir das), und die besitzen Frequenz/Wellenlänge (Energie) und Polarisation. Licht, das uns im Alltag begegnet, ist immer eine Durch- und Miteinander von Wellen verschiedener Frequenz/Wellenlänge, was man erkennt, wenn es durch ein Prisma gebrochen oder durch ein Strichgitter gebeugt wird: in beiden Fällen wird Licht in seine Frequenz-/Wellenlängenanteile aufgefächert (beim Prisma durch sog. Dispersion, beim Gitter durch Beugung), also gewissermaßen in seine Bestandteile zerlegt - und: wir nehmen ein Farbspektrum wahr. Weißes Licht wird in viele Farben zerlegt, fahles gelbes Licht in eine kleinere Anzahl, einfaches bspw. rotes oder blaues Licht nur in wenige. Daraus darf man nun schließen, dass tatsächlich die Frequenz/Wellenlänge des Lichts maßgeblich für die Farbwahrnehmung ist. Licht mit nur einer Frequenz-/Wellenlängenkomponente wird als monochromatisch, die dabei wahrgenommene Farbe als Spektralfarbe bezeichnet. Die Farbwahrnehmung von nicht leuchtenden Körpern wird durch die Frequenz-/Wellenlängenanteile des von ihnen reflektierten Lichts (und dem Licht der Leuchtquelle) bestimmt.
Das alles erklärt aber nocht nicht, warum wir überhaupt unterschiedliche Farben wahrnehmen, wenn wir Licht unterschiedlicher Frequenz/Wellenlänge sehen, und warum bestimmte Farben (bzw. Farbeindrücke) und Farbtöne, die wir sehen, nicht als Spektralfarben vorkommen (man denke an ein pastelliges Rosa). Letzteres zeigt uns jedenfalls, dass wir die Frequenz/Wellenlänge nicht alleine mit Farbe, wie wir sie kennen, identifizieren können. Vielmehr müssen wir es dabei mit irgendeiner Art von Vermischung von Spektralfarben zu tun haben. Zu weiteren Antworten führt uns erst der physiologische und der psychologisch-neurologische Aspekt:

- Abb. 2: Additive Farbmischung.
In der Netzhaut des menschlichen Auges befinden sich farbempfindliche Zellen dreierlei Typs, die sogenannten S-, M- und L-Zapfen. Sie enthalten verschiedene Varianten des Sehpigments Iodopsins, die unterschiedliche Absorptionskurven für Licht besitzen, s. Abb.1. Jeder der drei Zapfen-Typen reagiert somit auf einen unterschiedlichen Frequenz-/Wellenlängenbrereich. Zusätzlich zu den Zapfen enthält die Netzhaut die sog. Stäbchen-Zellen, die für das Nachtsehen (skotopisches Sehen) zuständig und weitaus lichtempfindlicher sind. Um die Stäbchen kümmern wir uns aber nicht.
Grob gesagt reagieren nun S-Zapfen auf blaues, M-Zapfen auf grünes und L-Zapfen auf rotes Licht. Die von den Zapfen durch physikalische Farbreize - Licht unterschiedlicher Frequenz/Wellenlänge - generierten Nervenimpulse (die biochemischen Details sind dabei einigermaßen umfangreich, aber für unsere Zwecke unwichtig) werden verschaltet und vom Gehirn zu den uns bewussten Farbeindrücken verarbeitet.
Also: alles Licht, das auf unsere Netzhaut fällt erzeugt je nach enthaltenen Frequenz-/Wellenlänegenanteilen unterschiedliche Erregungen der Zellen der drei Zapfentypen. Und das Tripel der L-, M-, und S-Stimulusgrößen - die sog. Farbvalenz (ein physiologischer Begriff für die Farbwahrnehmung) - erzeugt dann den Farbeindruck (der psychologisch-neurologische Begriff). Die Erregungszustände der drei Zapfen-Typen werden dabei vom zentralen Nervensystem (auch der Sehnerv ist Teil des ZNS!) zum Farbeindruck verarbeitet. Gleiche Erregung aller Zapfen wird als farblos (Weiß oder versch. Grautöne, das ist intensitätsabhängig) wahrgenommen. Die Frequenz- bzw. Wellenlängenempfindlichkeit der Zapfen-Typen überlagert sich, s. Abb. 1, es kommt also nie zur Erregung von nur einem Typ. Die ursprüngliche spektrale Verteilung des Lichts führt zu den drei Erregungswerten L(ong),M(edium) und S(hort) (die Namen beziehen sich auf die Wellenlängen der emfindlichen Bereiche), wobei ein Zapfen eine "integrale" Erregung durch alle ihn betreffenden Frequenzen erzeugt, d.h. dem jeweiligen Wert ist nicht mehr anzusehen, welche Frequenzen aus dem Empfindlichkeitsbereich des Zapfens beteiligt waren.
LMS-Farbraum
Der LMS-Farbraum ist nun definitionsgemäß die Menge aller Farbvalenztripel der Farben, die das menschliche Auge (zumindest das des Normalbeobachters, s.unten) wahrnehmen kann. Er wird also aufgespannt durch die physiologischen Reaktionstripel der Zapfen-Zellen. Insgesamt lässt sich somit jede durch eine beliebige spektrale Verteilung erzeugte Farbempfindung durch den LMS-Wert angeben. Oft wird auf die Gesamterregung L+M+S normiert, was zu den Größen l=L/(L+M+S), m=M/(L+M+S) und s=S/(L+M+S) führt. Da aber einerseits die Vermessung der Absorbtionskurven aus Abb.1 schwierig ist und andererseits die physiologischen Details früher gar nicht im Detail bekannt waren, hat man aus praktischen Gründen Empfindlichkeitskurven für drei spektrale Grundfarben durch Vergleichsmessung (das Auge als Nullinstrument) bestimmt und sie dem Normalbeobachter zugeordnet. Das führte dann zum CIE-Normvalenzsystem. Dass das überhaupt möglich ist, liegt an der additiven Weise, in der unser Sehapparat die 3 Farbreize verarbeitet. Heuristisch gewinnt man nämlich folgende Einsicht:
Die drei Farbempdindlichkeitskurven bilden eine Basis mithilfe der jeder durch eine spektrale Verteilung hervorgerufene Farbeindruck duch Komponenten in dieser Basis derart dargestellt werden kann, dass sich die Komponenten bei Farbmischung additiv verhalten. Oder in anderen Worten: unseren Farbeindrücke entsprechen Linearkombinationen von 3 Tristimulus(Hellempfindlichkeits)kurven. Die damit gewonnene lineare Struktur lässt dann die Wahl beliebiger anderer Basen zu.
Bemerkung: hätten wir mehrere Rezeptoren, würde unsere Farbwahrnehmung vielfältiger sein (um zu übertreiben: für jede Spektralverteilung einen Rezeptor, würde bspw. bedeuten, dass jede Spektralverteilung einen eigenen Farbeindruck invoziert).
Die Grassmanschen Gesetze fassen das zusammen (s. hier für eine genauere Fassung):
Grassmannsche Gesetze (genauer hier):
- Zwischen vier beliebigen, gegebenen Farben lässt sich durch Variation der Intensitäten von maximal drei (unabhängigen) Farben immer eine additive Mischung erzielen.
- Mischt man eine Farbe mit sich veränderndem Farbton mit einer Farbe, bei der der Farbton immer gleich bleibt, so entstehen nur Farben mit sich veränderndem Farbton.
- Der Farbton einer durch additive Farbmischung entstandenen Farbe hängt nur vom Farbeindruck der Ausgangsfarben, nicht jedoch von deren physikalischen (spektralen) Zusammensetzungen ab.
Wichtig: diese Sachverhalte sind empirischer Natur und gelten in dieser Form nur für die menschliche Farbwarnehmung. Dass 3 Farben genügen (oder besser: dass unsere Farbwahrnehmung solchermaßen eingeschränkt ist, dass durch nur 3 Reize der uns zugängliche Farbraum erschlossen wird), liegt zwar an den 3 unterschiedlichen Sehpigmenten, die anderen Eigenschaften folgen daraus aber keineswegs.
Für die weitere Behandlung von Farbräumen und Farbmodellen sind nun die Grassmanschen Gesetze - determiniert duch die Natur unserer Farbwahrnehmung - und die Farbvalenz, gedacht als Koordinaten in einem linearen dreidimensionalen Raum maßgebend.
Der CIE Normalbeobachter
Da die Farbwahrnehmung auch vom Blickfeld abhängt, werden alle Definitionen und Messungen (Vergleichsmessungen u.a.) auf den sog. CIE Normalbeobachter bezogen, um solche Abhängigkeiten auszuschließen.
Zur Definition soll ein Zitat aus Wikipedia für unsere Zwecke genügen: Dieser „gemittelte“ Beobachter blickt auf eine Fläche mit einem Sichtfeld von 2° mittig zur Hauptblickrichtung. Dieses Feld hat etwa die Größe einer 1-Euro-Münze, die man mit ausgestrecktem Arm vor sich hält. Diese Begrenzung wurde aus der Größe der Zone der höchsten Dichte der farbempfindlichen Photorezeptoren im Auge abgeleitet. Zusätzlich hat der CIE 1931 Normalbeobachter auch noch verschiedene sog. Empfindlichkeitskurven zugeordnet, vergleichbar mit den gleich beschriebenen L-, M-, und S-Absorbtionskurven, siehe dazu unter "CIE-Normvalenzsystem".
Es gibt mittlerweile auch modifzierte Nomarlbeobachter (bspw. CIE 1964), das soll uns aber nicht weiter kümmern.
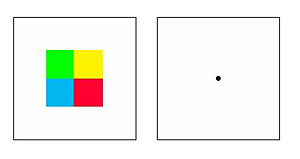
- Abb. 3: Sukzessivkontrast - Gegenfarbenmodell. Zum Vergrößern anklicken! (Quelle: Wikipedia).
Reizverarbeitung
Bei der ganzen bisherigen Diskussion haben wir verschwiegen, wie die Signalverarbeitung der optischen Reize hin zum optischen Eindruck mutmaßlich geschieht. Da wären die beschriebenen Valenztripel nur der erste Schritt. Dann kommt die Heringsche Gegenfarbentheorie (Erzeugung von rot-günen und blau-gelben Gegenfarbensignalen, die Gegenfarbentheorie wurde zwar auch früh (Mitte des 19. Jahrhunderts) mittels vielen Beobachtungen (Simultankontraste, Nachbilder - Sukzessivkontrast) entwickelt, aber erst im Rahmen der optischen Reizverarbeitung 100 Jahre später wieder aufgegriffen) zur Anwendung (Zonentheorie - von Kries, 1905). Und eigentlich ist alles viel komplizierter, weil im betroffenen Hirnareal, dem circulum geniculum laterale, gleich 7 Zelltypen an der Verarbeitung mit Berücksichtigung der Umfeldhelligkeit beteiligt sind. Das Dreifarbenmodell à la Grassmann alleine genügt zwar, um das quantifizierbare Farbvalenzmodell zu entwickeln, um allerdings die empfindungsgemäßen Größen wie Farbton, Helligkeit und Sättigung zu erfassen, braucht es dann ein Farberscheinungsmodell, das die Gegenfarbentheorie inkorperiert.
Bemerkung zum Gegenfarbenmodell: die jeweiligen Gegenfarben sind Rot-Grün und Gelb-Blau. Mittels Abb. 3 (zum Vergrößern anklicken!) kann man selbst ein kleines Experiment mit seinem Sehsinn anstellen, der erlebte Sukzessivkontrast sollte das Gegenfarbenmodell anschaulich motivieren. Nach der Zonentheorie (wegen Zonen aus unterschiedlichen Zellen) kombiniert die neuronale Signalverarbeitung die 3 unmittelbaren Farbreize zu den "Gegenfarbenwerten". Um eine Idee zu geben, notieren wir in RGB-Schreibweise (R, G und B seien tatsächliches Rot, Grün bzw. Blau) RGop=R−G (die Blau-Gelb-Achse liegt somit bei RGop=0, also bei R=G, B=0 (reines Gelb) und insbes. R=0=G (reines Blau)), YBop=(R+G)−B (analog für die Rot-Grün-Achse, statt R steht R+G (=Y)). Der achromatische (Grauwert) ist R+G+B. Unter "Empfindungsgemäße Farbräume" wird man sehen, wie sich das in speziellen LMS-Farbräumen darstellt.
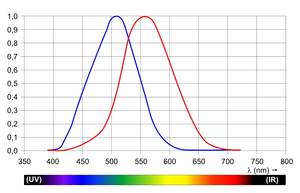
- Abb. 4: spektrale Hellempfindlichkeitskurve (Quelle: Wikipedia)
Photopische Hellempfindlichkeit
Das menschliche Tagsehen ist nicht für alle Wellenlängen des eintreffenden Lichts hinsichtlich der eintreffenden physikalischen Strahlungsleistung gleich empfindlich. Die rote Kurve in Abb. 4 - meistens mit V(λ) bezeichnet - gibt die Empfindlichkeit für das photopische Sehen, genormt auf 1, wieder. Sie ist im Wesentlichen die Summe der 3 Absorbtionskurven aus Abb.1. Ihre Bedeutung ist die Verknüpfung der strahlungsphysikalischen Größe "Strahlungsleistung" Φe mit der photometrischen Größe "Lichstrom" Φ (eigentlich definiert sie den Lichtstrom, siehe auch bei "Photometrie und Strahlung"):
Dabei ist km eine Konstante, das photometrische Strahlungsäquivalent. Wer sich übrigens wundert, warum über negative Wellenlängen integriert wird, dem sei versichert, dass das keine Rolle spielt, da alle Beteiligten dort keinen Beitrag zum Integral liefern.
V(λ) sieht bei jedem Menschen ein wenig anders aus (und sogar bei nur einem Menschen verändert sie sich zeitlich). Die tatsächlich verwendete CIE-standardisierte Kurve muss also aus einer Mittelung von Messungen bei hinreichend vielen Menschen entstehen. Zur Messung können mehrere Verfahren zur Anwendung kommen (was sich leider auch immer ein bisschen auf das Messergebnis auswirkt, aber egal). The Stophoto möchte hier kurz das sog. "Flimmerprinzip" erläutern. Ihm zugrunde liegt die Beobachtung, dass die Farbverschmelzungsfrequenz des Auges kleiner als seine Helligkeitsverschmelzungsfrequenz ist. Zur Messung von V(λ) werden nun an einer Stelle abwechselnd zwei formgleiche Lichter gezeigt, die sich aber in Farbe und Helligkeit unterscheiden. Bei einem der beiden Lichter wird Helligkeit und Farbe konstant gehalten (das "Vergleichslicht"), beim anderen (dem "Testlicht") wandert man den sichtbaren Frequenzbereich in kleinen Schritten ab. Bei jeder Frequenzeinstellung (also Spektralfarbe) verringert man dann die Helligkeit (Leistung) des Testlichts, bis zuerst nur mehr Helligkeits- und keine Farbschwankung und im Weiteren dann ein Minimum in der Helligkeitsschwankung auftritt. Je geringer dabei die Helligkeit des Testlichts bei der jeweiligen Frequenz ist, desto größer ist die Empfindlichkeit des Auges für jene Frequenz.
Psychometrische Helligkeitsfunktion
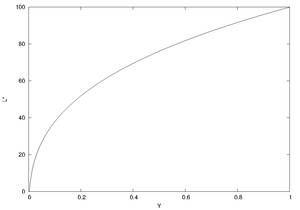
Mit der Helligkeit hat es noch eine weitere Sache auf sich, denn: ganz unabhängig von der Frequenz nehmen wir Helligkeit ungefähr logarithmisch wahr, was am Weber-Fechnerschen Gesetz liegt. Hier äußert es sich als psychometrische Helligkeitsfunktion. Zur Motivation: es ist der Helligkeitsunterschied dL*= dLp/Lp , wobei Lp die Leuchtdichte bedeutet, siehe "Photometrie und Strahlung". Durch Integration erhält man daraus die Funktion L*=log(k⋅L).
Eine realistischere Beschreibung für Körperfarben bei konstantem Adaptionszustand des Auges liefert allerdings eine Potenzfunktion, die dann als die erwähnte psychometrische Helligkeitsfunktion von der Commission internationale de l'éclairage (CIE) definiert wurde, siehe Abb. 5. Ermittelt wurde sie durch die empirisch gleichabständige Anordnung von verschieden hellen Grauproben von dunkel zu hell. Einem vollkommen matten Weiß unter gegebenen Beleuchtungsbedingungen wird dabei die Helligkeit 100 zugeordnet, genaueres siehe unter "Empfindungsgemäße Farbräume". Man spricht dann von relativer Helligkeit (lightness) anstelle von Helligkeit (brightness). Lightness ist also das Verhältnis von Helligkeit (brightness) zur Helligkeit (brightness) eines weißen Eindrucks. Abschließend sei noch erwähnt, dass mehrere Definitionen von Helligkeitsskalen existieren, bspw. die Munsell-Helligkeit, u.a., einige nurmehr von historischer Relevanz.
Farbigkeit, Buntheit, Sättigung, Weißpunkt
Die menschliche Farbwahrnehmung zerfällt bei Farbexperimenten auffällig in eine Hell- und eine Farbkomponente, die Tristimuluswerte sind dabei der Wahrnehmung nicht bewusst. Versuchspersonen beschreiben Farben und Farbänderungen hinsichtlich der wahrgenommenen Helligkeit und der "Farbigkeit", also so etwas wie dem Unterschied zu Grau (Unbunt). Dabei lassen sich 3 Begriffe abgrenzen: Farbigkeit (colorfulness), Buntheit (chroma) und Sättigung (saturation). Etwas unscharf (und besser geht's nicht, weil die Begriffe intuitiv sind) könnte man formulieren: Farbigkeit bezeichnet die Stärke des Unterschieds einer Farbe zu Grau (Unbunt), die Buntheit beschreibt den Unterschied bzw. das Verhältnis der Farbigkeit eines Farbeindrucks zum weißen Eindruck mit der gleichen Helligkeit und die Sättigung beschreibt, wie groß der Anteil der Farbigkeit eines Farbeindrucks am Farbeindruck selbst ist, also grob gesagt das Verhältnis von Farbigkeit des Eindrucks zu seiner Helligkeit. Näheres dazu hier...
(Relative) Helligkeit, Farbigkeit, Buntheit und Sättigung sind für die Farbwahrnehmung intuitive, aber grundlegende Begriffe, und es ist Aufgabe eines Color Adaption Models, sie aus den Tristimuluswerten der menschlichen Wahrnehmung konform - also die Wirkung von Farbexperimente vorhersagend - zu entwickeln.
In diesen Zusammenhang stellt sich auch der Weißpunkt: er entspricht jenem Farbvalenztripel, das die Wahrnehmung von Weiß erzeugt. In Farbdiagrammen spricht man auch vom Unbuntpunkt, wobei Weiß sozusagen das hellste mögliche Unbunt ist. Alle unbunten Punkte (von Schwarz über die versch. Graus bis zu Weiß) liegen in den versch. Farbmodellen dabei auf der sog. Unbuntgeraden, also dort, wo die Buntheit Null ist. Für Lichtfarben ist der Weißpunkt wenig interessant. Für Körperfarben hingegen, die ja eine externe Beleuchtung erfordern, hängt der Farbeindruck wesentlich von dieser Beleuchtung ab, und das ist sowohl für die Photographie als auch für die Reproduktion von Farben wichtig. Um hier Klarheit und Norm zu schaffen, wurden sog. Normlichter (standard illuminants) definiert. Der Weißpunkt entspricht dann der Farbvalenz des verwendeten Normlichts, näheres dazu hier...
Zu Photometrie und Strahlung, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile
Referenzen:
- Bergmann, Schaefer: Lehrbuch der Experimental Physik, Band 3, Optik. Walter deGruyter, Berlin 2004.
- Richard P. Feynman, Robert B. Leighton, Matthew Sands: Vorlesungen über Physik. Band I: Hauptsächlich Mechanik, Strahlung, Wärme. Oldenbourg Verlag, 4. Auflage 2001
- Gernot Hoffman, CIE Color Space, www.fho-emden.de/~hoffmann/ciexyz29082000.pdf