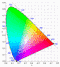
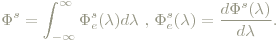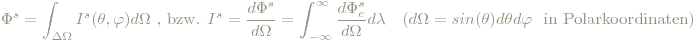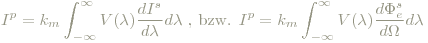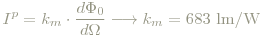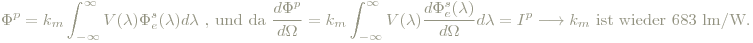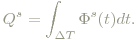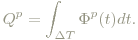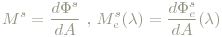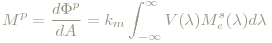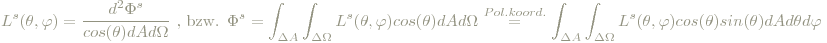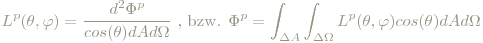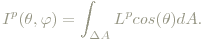Zu Farbsehen, CIE -Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

Photometrie und Strahlung

Hier folgt eine kleine Übersicht über wichtige Strahlungsgrößen im SI-System sowie ihre photometrischen Verwandten. Zwecks Lichtung des Begriffsdschungels sind Synonyme und die englischen Begriffe immer angegeben. Photometrische Größen sind mit ^"p", radiometrische mit ^"s" gekennzeichnet. Die unbestimmten Integrationsgrenzen stellen kein Problem dar, da alle Integranden nur auf einem endlichen Intervall von null verschieden sind. Generell ist die Notation nicht überaus exakt aber exakt genug um die Anschauung zu untermauern.

V(λ) steht sowohl für die skotopische als auch die photopische Hellempfindlichkeit, je nachdem ob man die Größen bezogen auf das Nacht- oder Tagsehen berechnen möchte.

Strahlungsleistung^s (Strahlungsfluss, radiant flux), spektraler Strahlungsfluss^s

Die Strahlungsleistung^s (der Strahlungsfluss) Φ^s ist die von elektromagnetischer Strahlung pro Zeiteinheit transportierte Energie. Einheit: Watt.

Der spektrale Strahlungsfluss^s Φ_^se ist die von elektromagnetischer Strahlung pro Zeiteinheit und Wellenlänge transportierte Energie. Einheit: Watt/Meter.

$\Phi^{s} = \int_{-\infty}^{\infty}\Phi^{s}_e(\lambda)d\lambda\textrm{ , } \Phi^{s}_e(\lambda)=\frac{d\Phi^s(\lambda)}{d\lambda}.$

Strahlungsintensität^s (Strahlungsstärke, radiant intensity)

Sie ist als diejenige Strahlungsleistung definiert, die in ein Raumwinkelement abgegeben wird und ist damit i.A. von der Abstrahlrichtung (θ,φ) (θ...Azimutalwinkel, φ...Horizontalwinkel) abhhängig, I^s=I^s(θ,φ).

$\Phi^s=\int_{\Delta\Omega}I^s(\theta,\varphi)d\Omega\textrm{ , bzw. } I^s=\frac{d\Phi^s}{d\Omega} = \int_{-\infty}^{\infty}\frac{d\Phi^s_e}{d\Omega}d\lambda\textrm{\ \ \ (} d\Omega=sin(\theta)d\theta d\varphi \textrm{\ \ in Polarkoordinaten)}$

Einheit: Watt/Steradiant. dΦ^s_e/dΩ könnte man mit Fug und Recht spektrale Strahlungsintensität nennen. Die der Strahlungsintensität zugeordnete photometrische Größe ist die Lichtintensität:

Lichtintensität^p (Lichtstärke, luminous intensity)

Gewichtet man die Strahlungsintensität mit der Hellempfindlichkeitsfunktion V(λ), erhält man per Definitionem die Lichtintensität. Einheit: Candela (cd).

$I^p = k_m\int_{-\infty}^{\infty}V(\lambda)\frac{dI^s}{d\lambda}d\lambda\textrm{ , bzw. } I^p = k_m\int_{-\infty}^{\infty}V(\lambda)\frac{d\Phi^s_e}{d\Omega}d\lambda$

Der Faktor k_m wird jetzt durch folgende Definition festgelegt:

„Die Einheit 1 Candela ist die Lichtstärke in einer bestimmten Richtung einer Strahlungsquelle, die monochromatische Strahlung der Frequenz 540·10¹² Hz aussendet und deren Strahlstärke in dieser Richtung 1/683 W pro Steradiant beträgt.“

Warum gerade 1/683 W/sr? Antwort: zur Herstellung von Konsistenz mit älteren Definitionen. Zum Wert von K gelangt man nun so: erstens bedeutet 540·10¹² Hz eine Wellenlänge von λ₀=555nm. Strahlung dieser Wellenlänge und der Leistung Φ₀entspricht einem spektralen Strahlungsfluss Φ₀ δ(λ−λ₀). In die Definition der Lichtintensität unter Berücksichtigung von (a) V(λ₀)=1 (bei 555nm liegt das Maximum von V(λ), s. Abb. 1) und (b) 1cd=1/683W/sr einsetzen gibt

$I^p=k_m\cdot \frac{d\Phi_0}{d\Omega}\longrightarrow k_m=683\textrm{ lm/W}$

: Abb.1: Lichtausbeute (oben), photopische (rot) und skotopische (blau) Hellempfindlicheiten (unten). Zum Vergrößern anklicken!

Dabei steht "lm" für Lumen, der Einheit des Lichstromes. Sie ist im SI-System über Candela definiert: 1 lm = 1 cd sr.

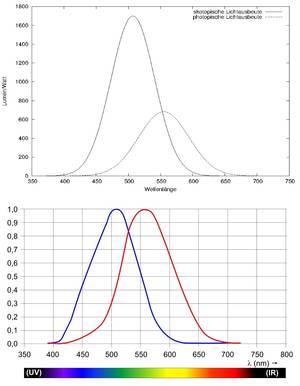
An dieser Stelle ist eine Bemerkung über Hellempfindlichkeit einerseits und Lichtausbeute (luminous efficacy) andererseits angebracht, s. nebenstehende Abb.1. Das untere Diagramm zeigt die bereits bei "Farbsehen" beschriebenen Hellempfindlichkeitskurven. Im oberen Diagramm sind die skotpische und die photopische Lichtausbeute dargestellt. Beide Diagramme sind verwandt: die photopische Lichtausbeute ist einfach K(λ):=683 lm/W⋅V(λ), also die photopische Hellempfindlichkeit multipliziert mit der eben gewonnen Konstante K, dem photometrischen Strahlungsäquivalent. Die skotopische Lichtausbeute ist K'(λ):= 1699 lm/W⋅V'(λ), wobei V'(λ) die photopische Hellempfindlichkeitskurve bezeichnet. Der Faktor 1699 lm/W ist dabei einfach 683 lm/W / V'(555nm). Es wird also die skotopische Helempfindlichkeit beim Maximum λ^p_max der photopischen (bzw. das Verhältnis V(λ^p_max):V'(λ^p_max) = 1:V'(λ^p_max)) zur Skalierung des Maximums der skotopischen Lichtausbeute herangezogen, was bewirkt, dass sich K(λ) und K'(λ) im Punkt (λ^p_max, 683lm/W) schneiden und damit die Definitionen, die k_m beinhalten für sowohl den skotopischen als auch photopischen Fall gelten, es ist nur jeweils V durch V' zu ersetzen. Damit genügt auch die oben gegebene Candela-Definition, die für den skotopischen und photopischen Fall gilt.

Lichtstrom^p (Lichtfluss, luminous flux)

Der Lichstrom Φ^p ist der mit der (photopischen/skotopischen) Hellempfindlichkeitsfunktion gewichtete (spektrale) Strahlungsfluss. Einheit: Lumen (lm), 1 lm = 1cd sr.

$\Phi^p = k_m\int_{-\infty}^{\infty}V(\lambda)\Phi^s_e(\lambda)d\lambda\textrm{ , und da }\frac{d\Phi^p}{d\Omega}=k_m\int_{-\infty}^{\infty}V(\lambda)\frac{d\Phi^s_e(\lambda)}{d\Omega}d\lambda=I^p\longrightarrow k_m \textrm{ ist wieder } 683\textrm{ lm/W.}$

Lichtmenge^p (luminous energy) und Strahlungsenergie^s (radiant energy)

Die Strahlungsenergie, die von einer Lichtquelle mit dem Strahlungsfluss in der Zeit ΔT ist klarerweise (s. Definition des Strahlungsflusses)

$Q^s=\int_{\Delta T}\Phi^s(t)dt.$

Die entsprechende photometrische Größe, die Lichtmenge, ist ganz analog definiert:

$Q^p=\int_{\Delta T}\Phi^p(t)dt.$

Spezifische Ausstrahlung^s (Ausstrahlungsstromdichte, Abstrahlungsstärke, radiant emittance) und spezifische Lichtausstrahlung^p (luminous emittance)

Unter der spezifischen Ausstrahlung M^s wird die Strahlungsleistung pro Fläche verstanden, die eine strahlende Oberfläche emitiert. Einheit: W/m². Als "spektrale" spezifische Ausstrahlung könnte man M^s_e bezeichnen:

$M^s=\frac{d\Phi^s}{dA}\textrm{ , } M^s_e(\lambda) = \frac{d\Phi^s_e}{dA}(\lambda)$

Und analog dazu wieder die photometrische Größe, die spezifische Lichtausstrahlung:

$M^p=\frac{d\Phi^p}{dA}=k_m\int_{-\infty}^{\infty}V(\lambda)M^s_e(\lambda)d\lambda$

Beleuchtungsstärke^p (illuminance) und Bestrahlungsstärke^s (irradiance)

Die zur spezifischen Ausstrahlung analoge Größe im Fall der Bestrahlung (sozusagen im Empfängerfall) ist die Bestrahlungssstärke, die zur spezifischen Lichtausstrahlung analoge Größe ist die Beleuchtungsstärke. Die mathematische Definitionen sind mit oben ident.

Strahldichte^s(radiance) und Leuchtdichte^p (Luminanz, luminance)

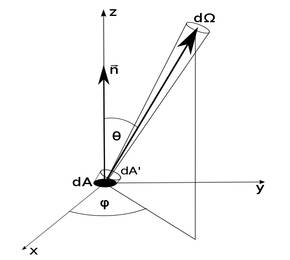
Will man den von einem Flächenelement eines Strahlers in eine bestimmte Richtung in ein Raumwinkelelement abgegebenen Strahlungsleistung ausdrücken, landet man bei der Strahldichte:

$L^s(\theta,\varphi)=\frac{d^2\Phi^s}{cos(\theta)dA d\Omega}\textrm{ , bzw. } \Phi^s=\int_{\Delta A}\int_{\Delta\Omega}L^s(\theta,\varphi)cos(\theta)dAd\Omega \stackrel{Pol.koord.}= \int_{\Delta A}\int_{\Delta\Omega}L^s(\theta,\varphi)cos(\theta)sin(\theta)dAd\theta d\varphi$

: Abb. 2: zur Strahl- und Leuchtdichte. Zum Vergrößern anklicken!

wobei θ und φ der Azimutal- und Horizontalwinkel der betrachteten Abstrahlrichtung ist.Einheit: W/(m²sr).

An dieser Stelle bedarf es vielleicht wieder einer Erläuterung, siehe dazu Abb. 2: ein Beobachter sitze irgendwo entlang der Strahlrichtung (Θ,φ), die Koordinaten sind dabei so gewählt, dass die Flächennormale eines gedachten Flächenelements dA mit der Beobachtungsrichtung den Winkel θ einschließt. Das für den Beobachter aus der Richtung (Θ,φ) sichtbare Flächenelement ist die Projektion dA' = cos(Θ)dA. Die Strahldichte ist dann der Strahlungsfluss pro Raumwinkel und pro für den Beobachter "wirksames" (sichtbares) Flächenelement.

Die spektrale Strahldichte ist die auf Wellenlänge/Frequenz bezogene Strahldichte.

Prominentes Beispiel für eine (spektrale) Strahldichte ist die des schwarzen Strahlers, erstmals von Max Planck 1900 angegeben. Ihrer Herleitung liegt die fundamentale und die gesamte moderne Physik beeinflussende Annahme zugrunde, dass die Energie eines Oszillators nur "in Portionen" (Quanten) aufgenommen und abgegeben werden kann.

Ein strahler mit L^s = const (also richtungsunabhängiger Strahldichte) heißt lambertscher Strahler. Insbesonders ist ein schwarzer Strahler ein lambertscher Strahler.

Die Leuchtdichte ist die zur Strahldichte analoge photometrische Größe, der geometrische Sachverhalt aus Abb.2 bleibt der gleiche. Einheit: cd/m².

$L^p(\theta,\varphi)=\frac{d^2\Phi^p}{cos(\theta)dA d\Omega}\textrm{ , bzw. } \Phi^p=\int_{\Delta A}\int_{\Delta\Omega}L^p(\theta,\varphi)cos(\theta)dAd\Omega$

Der Zusammenhang mit der Lichstärke ist (vergleiche mit weiter oben)

$I^p(\theta,\varphi)=\int_{\Delta A}L^pcos(\theta)dA.$

Die Leuchtidchte (Luminanz) wird gerne mit Helligkeit gleichgesetzt, was schon wegen des Helmholtz-Kohlrausch-Effekts (je "näher" eine Farbe der Spektralfarbe kommt, desto heller wirkt sie) nicht ganz richtig ist. Außerdem entsprechen Leuchtdichtedifferenzen nicht gleichen Helligkeitsdifferenzen, was am Weber-Fechnerschen Gesetz liegt. Vielmehr wird zur Bewertung von Helligkeit die psychometrische Helligkeitsfunktion herangezogen, siehe unter Farbsehen.

Zu Farbsehen, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

Referenzen:

Bergmann, Schaefer: Lehrbuch der Experimental Physik, Band 3, Optik. Walter deGruyter, Berlin 2004.

the stophoto

Über Farben

Kompression und JPEG

Was man immer schon über Schärfentiefe wissen wollte...

Zu Farbsehen, CIE -Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

Photometrie und Strahlung

Strahlungsleistung^s (Strahlungsfluss, radiant flux), spektraler Strahlungsfluss^s

Strahlungsintensität^s (Strahlungsstärke, radiant intensity)

Lichtintensität^p (Lichtstärke, luminous intensity)

Lichtstrom^p (Lichtfluss, luminous flux)

Lichtmenge^p (luminous energy) und Strahlungsenergie^s (radiant energy)

Spezifische Ausstrahlung^s (Ausstrahlungsstromdichte, Abstrahlungsstärke, radiant emittance) und spezifische Lichtausstrahlung^p (luminous emittance)

Beleuchtungsstärke^p (illuminance) und Bestrahlungsstärke^s (irradiance)

Strahldichte^s(radiance) und Leuchtdichte^p (Luminanz, luminance)

Zu Farbsehen, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

the stophoto

Über Farben

Kompression und JPEG

Was man immer schon über Schärfentiefe wissen wollte...

Zu Farbsehen, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

Photometrie und Strahlung

Strahlungsleistungs (Strahlungsfluss, radiant flux), spektraler Strahlungsflusss

Strahlungsintensitäts (Strahlungsstärke, radiant intensity)

Lichtintensitätp (Lichtstärke, luminous intensity)

Lichtstromp (Lichtfluss, luminous flux)

Lichtmengep (luminous energy) und Strahlungsenergies (radiant energy)

Spezifische Ausstrahlungs (Ausstrahlungsstromdichte, Abstrahlungsstärke, radiant emittance) und spezifische Lichtausstrahlungp (luminous emittance)

Beleuchtungsstärkep (illuminance) und Bestrahlungsstärkes (irradiance)

Strahldichtes (radiance) und Leuchtdichtep (Luminanz, luminance)

Zu Farbsehen, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

Zu Farbsehen, CIE -Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile

Strahlungsleistung^s (Strahlungsfluss, radiant flux), spektraler Strahlungsfluss^s

Strahlungsintensität^s (Strahlungsstärke, radiant intensity)

Lichtintensität^p (Lichtstärke, luminous intensity)

Lichtstrom^p (Lichtfluss, luminous flux)

Lichtmenge^p (luminous energy) und Strahlungsenergie^s (radiant energy)

Spezifische Ausstrahlung^s (Ausstrahlungsstromdichte, Abstrahlungsstärke, radiant emittance) und spezifische Lichtausstrahlung^p (luminous emittance)

Beleuchtungsstärke^p (illuminance) und Bestrahlungsstärke^s (irradiance)

Strahldichte^s(radiance) und Leuchtdichte^p (Luminanz, luminance)