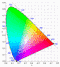
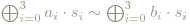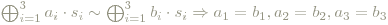Zu Farbsehen, Photometrie und Strahlung, CIE-Normvalenzsystem, Empfindungsgemäße Farbräume, Technische Farbräume und ICC-Profile
Grassmannsche Gesetze
Die Grassmannschen Gesetze lassen sich auch formaler beschreiben. Dazu geben wir ein paar Definitionen:
Grassmann-Struktur: sei S eine Menge, "⊕" eine Abb. von SxS nach S, "⋅" eine Abb. von R+xS nach S und "~" eine Äquivalenzrelation auf S. Das Quadrupel (S,⊕,*,~) heißt Grassmann-Struktur, wenn folgende Eigenschaften zutreffen:
- (s1⊕s2)⊕s3=s1⊕(s2⊕s3), s1⊕s2=s2⊕s1 und s1⊕s3 =s2⊕s3 → s1=s2 für alle s1,s2,s3 ∈ S
- "⋅" erfüllt die Eigenschaften einer Multiplikation mit einem Skalar
- s1~s2 ⇔ s1⊕s3 ~ s2⊕s3 für alle s1,s2,s3 ∈ S
- s1~s2 → a⋅s1 ~ a⋅s2 für alle s1,s2 ∈ S, a ∈ R+
- Zu allen s1,s2,s3,s4 ∈ S existieren a1,a2,a3,a4,b1,b2,b3,b4 ∈ R+, mit ai≠bi für mindestens ein i ∈ {0,1,2,3} sodass:
- Es gibt s1,s2,s3 ∈ S, sodass gilt:
für beliebige a1,a2,a3,b1,b2,b3 ∈ R+.
Sei nun (S,⊕,*,~) eine Grassmann-Struktur. Dann gilt der Repräsentationssatz: zu jeder Grassmann-Struktur existiert ein reeller Vektorraum V, ein konvexer Kegel K⊆V und eine Abb. Φ: S→K, sodass für alle s,s' ∈ S, a ∈ R+und v ∈ V gilt:
- Φ(s⊕s') = Φ(s) + Φ(s')
- Φ(a⋅s)=aΦ(s)
- s~s' ⇔ Φ(s)=Φ(s')
- es existieren t,t'∈S, sodass v = Φ(t)-Φ(t')
Φ heißt Grassmann-Homomorphismus. Es gilt außerdem der Eindeutigkeitssatz: zu jeder Grassmann-Struktur und Grassmann-Homomorphismen Φ,Φ' (auf konvexe Kegeln K,K' in V bzw.V') existiert eine bijektive lineare Abb. T: V→V' mit: für alle s∈S gilt T(Φ(s))=Φ'(s).